Let’s consider conditional independence.
I would recommend an example below which is the one of the best example to explain conditional independence intuitively.
I’ve heard an on-line machine learning lecture from Prof. Il-Chul Moon who is the professor at KAIST. I would like to quote an picture from that lecture (3.2)
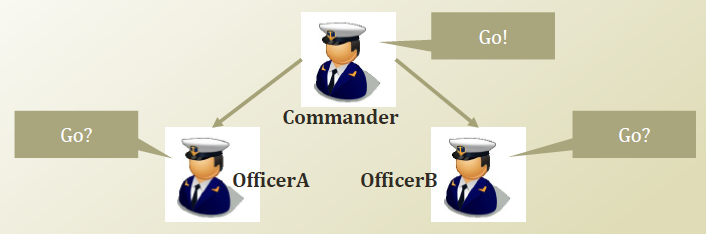
There is an commander who can order belonged officers to go forward and two officers A, B. If officerA found officerB was going forward, then what is about the probability that officerA also go forward? It may be greater than the probability that officerA go forward without any observations. (He noticed officerB was going forward and thought that there were some commands to go).
So, P(OfficerA \, = \, Go \, | \, OfficerB \, = \, Go)\, > \, P(OfficerA\, = \, Go)
This is not marginally independent!
On the other hand, if we assume that officerA got the command from the Commander and even saw the officerB went forward. What’s the difference?
In this case, the act of officerB (go forward) couldn’t affect the act of officerA (go forward), then we can say this is conditionally independent.
P(OfficerA\, = \, Go\, | \,OfficerB\,=\,Go, Commander\, = \, Go(Yawl))
=P(OfficerA\,=\,Go\, | \, Commander\,=\,Go)
We can define conditional independence in formal. [refered]
x_1 is conditionally independent of x_2 given y
(\forall x_1,x_2,y) \, P(x_1|x_2,y)=P(x_1|y) \cdots (*)Consequently, the above asserts
P(x_1, x_2|y) = P(x_1|y) \cdot P(x_2|y)
I would like to derive the equation above.
From the (*),
P(x_1|x_2,y)= \dfrac {P(x_1, x_2, y)}{P(x_2,y)} = P(x_1|y)\Longrightarrow P(x_1,x_2,y) = P(x_2,y) \cdot P(x_1|y)
\Longrightarrow P(x_1,x_2,y) = P(x_2|y) \cdot P(y) \cdot P(x_1|y)
We knew P(x_1,x_2|y)= \dfrac {P(x_1,x_2,y)} {P(y)}
\therefore P(x_1,x_2|y) = P(x_1|y) \cdot P(x_2|y)
