Conditional Probability is defined as below.
P(B|A) = \dfrac{P( A \cap B)}{P(A)}
It implies that probability space should be restricted in A to get P(B|A) .
It can be shown as like a picture below.
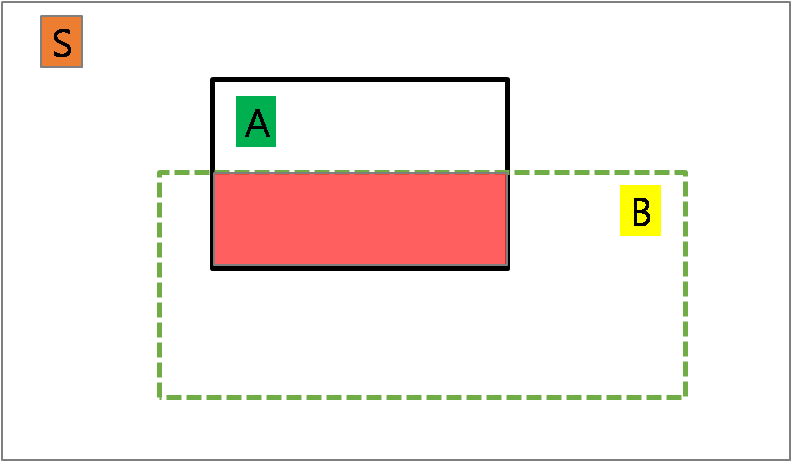
Let’s consider the independence of events.
If we assume that there are 10 balls in a box. (# of black balls = 7, # of red balls = 3)
We can find the probabilities in two different cases.
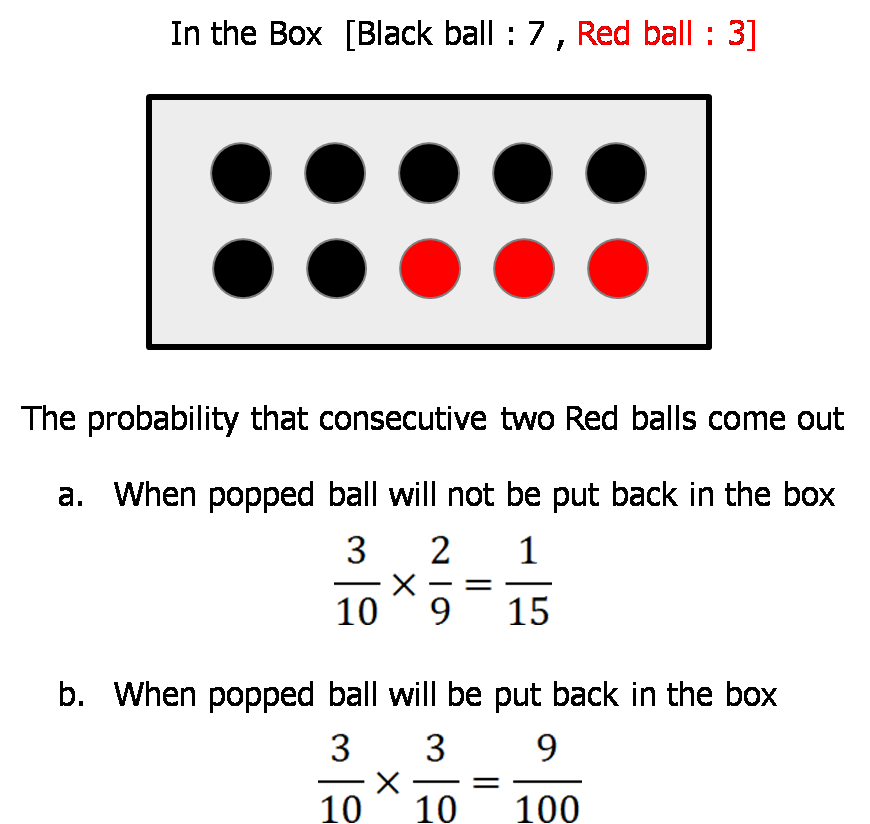
We can say a. is a dependent trial, but b. is an independent trial.
In probabilistic expressions for above descriptions are like this.
P(A) \times P(B|A)
The second trial was independent of the first trial. Frankly speaking I really would like to introduce independence between two events here, but this is not a appropriate example for that. For the reason why is that, I will explain that here.
