앞서 가능도(likelihood) 대한 글에 이어서 “메이저리그 야구 통계학” 에서 소개하는 재미난 예제를 살펴볼까 한다.
이 글의 일부는 “메이저리그 야구 통계학” 책의 4장 ‘상관관계는 인과관계가 아니다’ 절을 직접 인용하고 있음을 미리 밝혀둔다. 이 포스트에 사용된 예제 소스는 Github 에서 확인 할 수 있다.
1. 출루율이 정해진 상황에서의 다섯번 타석에 들어섰을 때 두 번 출루할 확률

조이 보토 (Joey Votto) 선수는 2015시즌 .460 이라는 엄청난 출루율을 달성하였다. 당시에 추신수 선수와 한 솥밥을 먹으며 국내 팬들에게도 익숙한 출루머신이었다. 조이 보토 선수가 타석에 들어섰을 때, 출루할 확률은 46%라고 기대된다.
타석에서 이러한 확률을 가진 조이 보토 선수가 2번 혹은 3번 타자로서(당시 1번은 대개 추신수였다.) 한 게임에 보통 다섯 번의 타석 기회가 있는데, 한 게임에서 출루를 두 번 할 확률은 얼마나 될 것인가?
잠깐, 혹시라도 야구에 대해 익숙히 않은 분은 출루율이 무엇인지 헷갈릴 수 있기 때문에 잠시 소개하고 넘어가겠다. 출루율이란,
타자가 타석에서 베이스로 얼마나 많이 살아 나갔는지를 백분율로 나타낸 수치이다. 영어로는 온베이스퍼센티지(on base percentage)라고 한다. 줄여서 OBP라고도 한다. 주로 1번 타자에게 높은 출루율이 요구된다. 이는 1번 타자가 출루함으로써 다음 타자의 부담이 줄어들 수 있으며 상대팀에게는 첫 타자부터 출루시켰다는 압박감을 줄 수 있기 때문이다.
[산출 공식](안타+데드볼+베이스온볼스)÷(타수+데드볼+베이스온볼스+희생플라이)
출루한 횟수를 타석에 오른 횟수로 나눈다. 이때 타자가 안타를 쳐 출루한 것은 물론이고, 데드볼(몸에 맞는 공, 死球)과 베이스온볼스(사구, 四球)로 인해 출루한 것 역시 출루 횟수에 포함한다. 계산하여 나온 수를 소수점 아래 넷째 자리에서 반올림하여 소수점 아래 셋째 자리까지 표시한다. (두산백과)
출루율로 전체 시행(게임에 등판한 수) 대비 해당 조건이 충족되어 성공한 시행의 빈도수 비율을 확률로 정의할 수 있다. 확률을 이야기할 때 항상 같이 언급해야 하는 내용이 확률분포다.
아마 통계에 대한 지식이 조금 있으신 분들이라면 출루율(OBP; On base Percentage) 을 성공확률 p 로 하는 이항(binomial) 분포를 가정할 수 있을 것이다. 즉 여러번의 시행은 서로 독립적이며 각 시행이 성공할 확률은 p , 실패할 확률은 1-p 를 갖는다.
총 n 번의 시도 중에서 k번은 성공하고 n-k 번은 실패하게 된다.
이를 확률로 표현하면 이항분포의 확률분포함수가 도출되는데 다음과 같다.
Pr(k;n,p) = Pr(X=k) =\binom{n}{k} p^{k}(1-p)^{n-k} \cdots (*)for k = 0, 1, 2,\cdots,n
where \binom{n}{k} = \dfrac{n!}{k!(n-k)!}
타순에서 2번을 치는 보토 선수가 한 경기당 타석에 다섯번 들어서는 것이 일반적이며, 그의 출루율을 감안할 때 출루를 두 번 할 확률이 가장 높으며, 출루를 못 하거나 전 타석에서 모두 출루할 경우는 매우 희박한 모습을 머릿속에 그리고 있다면 이항확률분포를 머리속에 그리고 있는 것이다.
위 (*) 의 이항확률분포함수에서 n=5, k=2, p=0.460 을 대입해보면,
^5C_2 \times {0.460}^2 \times {0.540}^3 = 33.32 % 가 나온다.
직접 식으로 구하는 대신 난수를 발생시켜 (출루율의 확률로서) 나온 결과를 확인해 보았다.

위의 확률분포함수를 통해서 구한 식과 상당히 유사한 것을 확인할 수 있다.
2. 최대우도 추정법; 다섯 번의 타석에서 두 번 출루할 확률이 가장 높은 선수의 출루율
앞에서 조이 보토 선수의 출루율을 알고 있는 상황에서 5번 타석에서 2번 출루할 확률을 구했다면, 이번에는 5번 타석에서 2번 출루한 상황을 관찰했을 때 이 가능성이 가장 높은 조건인 출루율 모수 (parameter) 를 구해보자.
보토 선수의 출루율이 알려져 있지 않은 경우, 그가 다섯 번의 타석에서 두 번 출루하는 것을 옆에서 지켜보고, 앞으로도 다섯 번의 타석에서 두 번 출루할 수 있는 확률을 극대화하는 데 필요한 출루율을 4할이라고 역추적했다면, 4할은 다섯 번의 타석에서 두 번의 출루 확률을 극대화하는 우도(likelihood)가 된다.
확률과의 가장 큰 차이는 확률은 한 사건(다섯 번의 타석에서 두 번 출루)의 조건인 출루율을 알고 있어서 다섯 타석에서 두 번의 출루가 발생할 빈도에 주목할 수 있지만, 모수인 출루율을 모르는 상황에서는 다섯 번의 타석 중에서 두 번의 출루가 발생 할 수 있는 빈도가 가장 높게 만드는 조건을 찾아야 하며, 그 조건이 우도다.
지금부터는 거꾸로 다섯 번의 타석 중 두번만 출루할 가능성을 가장 높이는 출루율 모수를 찾기 위해 이항확률분포함수 에 전체 시행수인 5와 2를 대입한다.
※ “두번의 출루” 사건을 TWICE 라고 하자.
P(TWICE)= \binom{5}{2} \times {OBP}^2 \times (1-OBP)^3(OBP = On Base Percentage;출루율)
최대우도추정법에서는 로그 함수가 단조증가하는 성질을 활용하여 확률 식에 로그를 취해서 기울기가 0인 (즉 한번 미분한 값이 0인 지점) 지점을 최대 우도 발생점으로 구하게 된다.
ln(P(TWICE))=ln( \binom{5}{2} \times OBP^2 \times (1-OBP)^3 = ln10 + 2lnOBP + 3ln(1-OBP)추정할 모수인 OBP(출루율)에 대해 미분하면,
\dfrac{\partial ln(P(TWICE))}{\partial OBP} = \dfrac{2}{OBP} - \dfrac{3}{1-OBP} = 0위 식을 정리하면 OBP = \dfrac{2}{5} =0.4 이 된다.
직관적으로도 그러하다고 생각한 값을 수학적으로 얻어냈다.
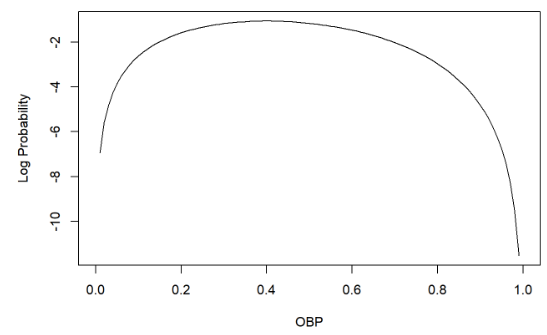
3. 출루율에 따른 다섯 번 타석에 들어섰을 때 출루할 6가지 경우의 수
타석에 다섯 번 들어섰을 때, 출루하는 경우는 0, 1, 2, 3, 4, 5 의 여섯 가지 경우의 수를 가진다.
출루율 4할인 선수가 다섯 번의 타석에서 두 번 출루할 확률은 34.56% 로 가장 높은 것으로 계산된다. (이항분포를 따를 때)
아래 여섯 가지 경우의 수의 확률 값을 계산했으며,
막대그래프로 나타내보면, 세 번재 막대 (2번 출루하는 경우)가 가장 높고 우측으로 약간 기울어진 분포가 나타난다.
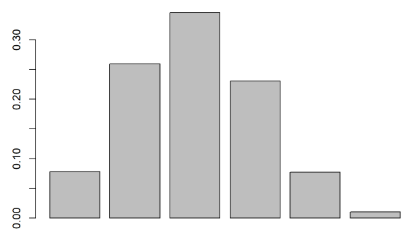
이항분포에서 분포의 모양을 정하는 원인은 단 두 가지다. 선수의 출루율과 시행횟수가
확률분포 모양을 정하며, 출루율 3할 선수와 2할 선수, 4할 선수의 확률분포 모양은 달라
질 수 밖에 없다.
출루율이 2할, 3할, 4할, 5할인 경우의 확률분포 모양을 비교해 보자.
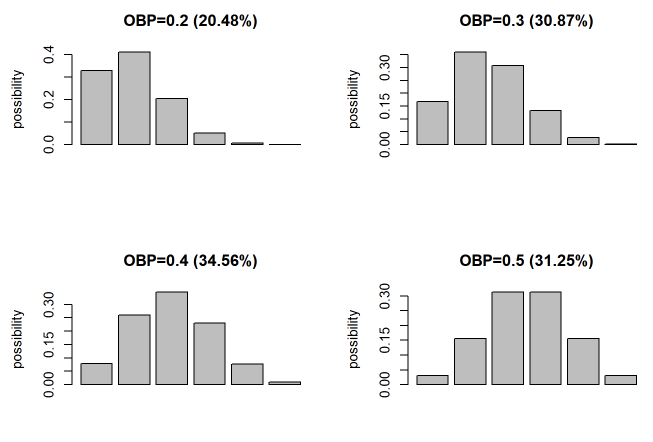
출루율이 2할인 선수가 다섯 번의 타석에서 2개를 출루 할 수 있는 확률은 20.48이고, 3할 선수는 30.87%, 5할 타자는 31.25% 인 것으로 계산되었다.
4. 선수가 100 경기를 뛴 것을 관찰 했을때, 최대우도추정 값은 어떻게 구할까?
문득 5 타석에 들어선 것을 한 번만 관찰한 것이 아니라면 어떻게 될까하는 의문이 들었다. 실제와 유사하게 5타석에 들어서 2번 출루할 수도 있고, 1번 출루할 수도 있고, 운이 좋은 날은 5번 모두 출루할 수도 있을 것이다.
P_{OBP} 를 모 파라미터인 선수의 출루율이라 가정하면 likelihood 의 정의에 따라,
L(P_{OBP}|x_1,x_2,\cdots,x_n)= L(P_{OBP}|x_1) \times L(P_{OBP}|x_2) \times \cdots \times L(P_{OBP}|x_n)이라고 할 수 있다.
- 5번 타석에서 i 번 출루하는 횟수를 k_i 라고 정의하자.
- 각 i 번의 출루가 관측된 횟수가 n_i 라고 한다면 n_0 + n_1 + n_2 + n_3 + n_4 + n_5 = 100 이다.
조금 복잡하지만 100번의 관측(경기)를 통해서 6가지 출루 경우들의 관측횟수를 반영하면 우도함수는 다음과 같이 얻을 수 있다.
L(P_{OBP}|x_1,x_2,\cdots,x_n) = {\binom{5}{k_0}}^{n_0} {P_{OBP}}^{k_0n_0} (1-P_{OBP})^{(5-k_0)n_0}\times{\binom{5}{k_2}}^{n_2} {P_{OBP}}^{k_2n_2} (1-P_{OBP})^{(5-k_2)n_2}
\cdots \times{\binom{5}{k_5}}^{n_5} {P_{OBP}}^{k_5n_5} (1-P_{OBP})^{(5-k_5)n_5}
양변에 로그를 취해서 정리하면,
ln(L(P_{OBP}|x_1,x_2,\cdots,x_n)) = n_0ln{\binom{5}{k_0}} + k_0n_0ln(P_{OBP}) + (5-k_0)n_0ln(1-P_{OBP})+ n_2ln{\binom{5}{k_2}} + k_2n_2ln(P_{OBP}) + (5-k_2)n_2ln(1-P_{OBP})
\cdots + n_5ln{\binom{5}{k_5}} + k_5n_5ln(P_{OBP}) + (5-k_5)n_5ln(1-P_{OBP})
가 된다. P_{OBP} 에 대해서 미분을 취해서 0으로 놓고 전개하면,
0 =\dfrac {\displaystyle\sum_{i=0}^{5} {k_in_i}}{P_{OBP}} - \dfrac {\displaystyle\sum_{i=0}^{5} {(5-k_i)n_i}}{1-P_{OBP}}
\Longrightarrow(1-P_{OBP}){\displaystyle\sum_{i=0}^{5} {k_in_i}} = {P_{OBP}}{\displaystyle\sum_{i=0}^{5} {(5-k_i)n_i}}
\therefore P_{OBP} =\dfrac {\displaystyle\sum_{i=0}^{5} {k_in_i}}{\displaystyle\sum_{i=0}^{5} {k_in_i} + \displaystyle\sum_{i=0}^{5} {(5-k_i)n_i}}
위의 식을 바탕으로 일반적인 출루율일 경우, 매우 좋은 출루율일 경우, 매우 안 좋은 출루율을 가정하고 n_0, n_1, n_2, n_3, n_4, n_5 값들을 시뮬레이션 해 보았다.
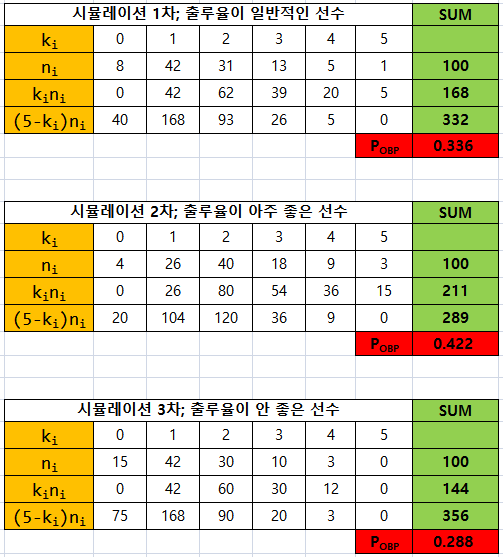
위와 같이 출루율 (P_{OBP})과 타석(n)에 따른 출루 횟수(k) 를 파라미터로 하는 이항확률분포함수를 가정하고, 100번의 게임에 대한 관측값을 변화시켜 가면서, 모수의 파라미터인 출루율을 최대우도추정법(Maximum Likelihood Estimation)을 사용하여 추정할 수 있었다.
