2022.2.15.
Lecture#1 Gaussian Processes and Neural Processes, 이주호 교수, KAIST
Bayesian Regression : \theta \sim p(\theta) \text{: uncertainty} 가정.
p(y_*|x_*, X, y) = \int p(y_*|x_*,\theta) p(\theta | X, y) d \thetadata uncertainty (aleatoric) due to observation noise : p(y_*|x_*,\theta)
model uncertainty (epistemic) due to the parameter uncertainty : p(\theta | X, y)
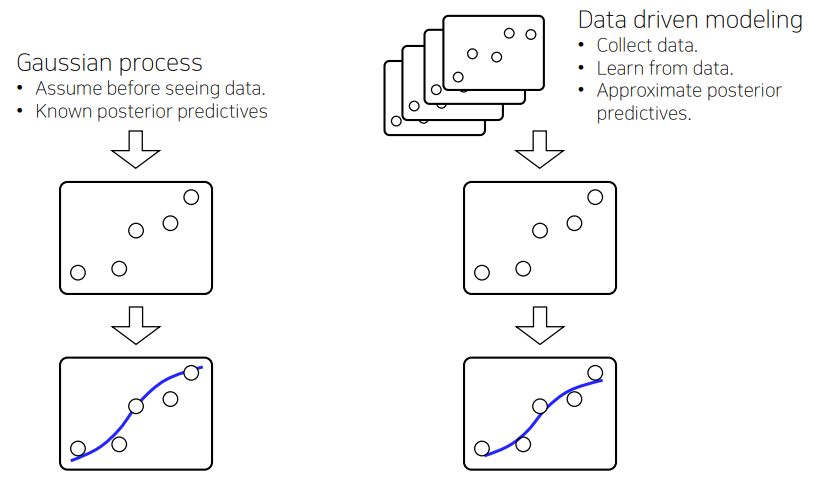
Why don’t we assume priors on functions directly?
A prior over functions = a prior over infinite dimensional vectors = a collection of infinitely many random variables
A stochastic process is a collection of random variables indexed by some input set.
\{ f(x) \}_{x \in R}Finite-dimensional distributions of stochastic processes
Gaussian processes (GP) : a stochastic process whose finite-dimensional distribution is a multivariate Gaussian.
\text{For any } n \in N, \mu(x) = E[f(x)]. K(x, x') = E[(f(x-\mu(x))(f(x' - \mu(x'))]
Neural Process (NP) : Using neural networks to construct stochastic processes, a type of “implicit” stochastic processes
f(x) = g(x, z; \theta), z \sim p(z)Conditional Neural Process -> Neural Processes
Other NPs
– Attentive neural processes, Kim et al, 2019
– Sequential NP, Singh et al, 2019
– Convolutional CNP, Gordon et al, 2020
– EquivCNP, Kawano et al, 2021
– Bootstrapping (A)NP, Lee et al, 2020
Lecture#2 심층학습기반의 자연어처리 동향, 이근배 교수, POSTECH
2022.2.16
Lecture#3 Kernel based Embedding, 신현정 교수, 아주대학교
0. Kernel Method
Linear method + embedding in feature space
1. Hilbert Space
Topological Space ⊃ Metric Space ⊃ Normed Vector Space ⊃ Inner Product Space ⊃ Hilbert Space
A Hilbert space is a generalization of finite dimensional vector spaces with inner product to possibly infinite dimension. Most of interesting infinite dimensional vector spaces are function
spaces. Hilbert spaces are the simplest among such spaces.
It allows linear algebra and calculus to spaces (Ex) differential and integral calculus
Any continuous linear functional on a Hilbert space is given by an inner product with a vector (Riesz Representation Theorem)
Riesz Representation Theorem
Let H be a Hilbert space over H. If f ∈ H*, then there exists a unique vector u in H such that
f(\nu) = < \nu, u >_H \text {for all } \nu \in H
< \nu, u >_H represents the evaluation of f at \nu, f(\nu)
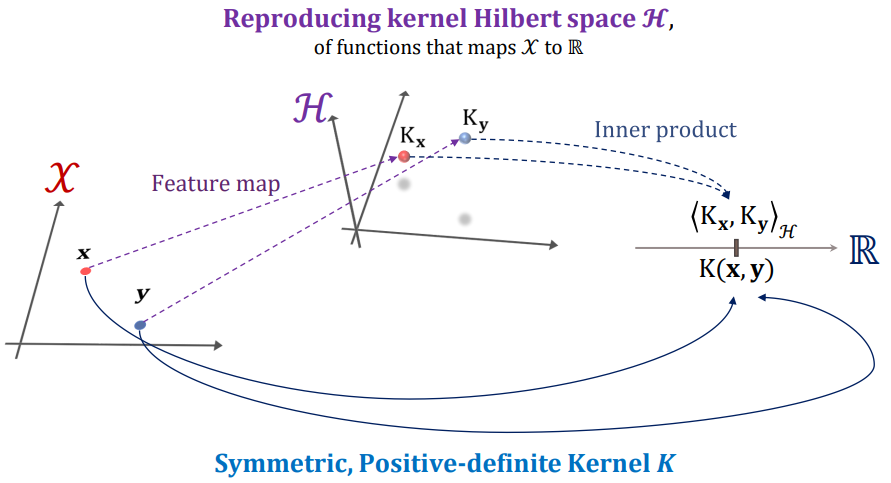
Reproducing Kernel Hilbert Space
A Hilbert space, in which each point of the space is a continuous linear function
H = \{ f(z): \sum^k_{j=1} \alpha_j \phi_{x_j} (z), \forall k \in N_+ \text {and } x_j \in X \}
Definition of “Reproducing”
f(x) = < f, \phi_x >_Hwhere for all functions f \in H \text {and } \phi_x \in H is the mapping function
Mercer’s Theorem
If K ∈ H is a continuous symmetric and positive semidefinite function,
K(u, v) = \sum^{\infty}_{i=1} \lambda_i \psi_i(u) \psi_i(\nu) = < \phi(u), \phi(\nu)>_H = \phi(u)^T \phi(\nu)
Symbolically, data points are mapped to RKHS feature space
Operationally, they are only evaluated with inner products
References
Learning with Kernels, Bernhard Scholkopf and Alexander J. Smola, The MIT Press
Convex Optimization, John Shawe-Taylor and Nello Cristianini, Cambridge University Press
Lecture#4 Random Projections and Fourier Features, 최승진 교수, BARO AI
2022.2.17
Lecture#5 Forecasting Future of Video Frames, 홍승훈 교수, KAIST
관측 프레임 : Context Frame x_1, x_2, ..., x_C \rightarrow x_{1:C}
Prediction : x_{C+1}, ..., x_T \rightarrow x_{C+1:T}
p(x_{C+1}, ..., x_T | x_1, x_2, ..., x_C) \rightarrow p(x_{C+1:T} | x_{1:C})
Videos is a Sequences => Sequence Modeling
Challenges
– Continuous
– High-Dimensional Sequence
Prediction can be transformed to Synthesis
p(x_{1:T} = p(x_{C+1:T} | x_{1:C}) p(x_{1:C}) = p(x_{ \leq T} )
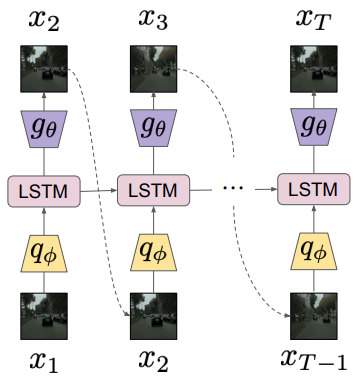
Image Autoregressive Model
p(x_{ \leq T }) = p(x_T | x_{< T}) p(x_{< T}) = \prod^T_{t=1} p(x_t | x_{< t})
LSTM Model
p(x_t | x_{\leq t}) = g_{\theta}(h_t)
– Stochasticity 가 없다.
– Error 가 축적된다.
– 계산 비용 높다
– 일반화가 어렵다.
Research Agendas in VP
– Stochastic Models
– State-space Models
– Decomposing factors of variations
– Discrete Representation (Vector Quantization)
– Continuous-time Models
① Stochastic Models
– Denton et al., Stochastic Video Generation with a Learned Prior
② State-space Models
– Villegas et al., High Fidelity Video Prediction with Large Stochastic Recurrent Neural Networks
– Structured Inference Networks for Nonlinear State Space Models, In AAAI, 2017
– Clark et al., Adversarial Video Generation On Complex Datasets
– Tian et al., A Good Image Generator Is What You Need For High-Resolution Video Synthesis
– Franceschi et al., Stochastic Residual Video Prediction
③ Decomposing factors of variations
– Tulyakov et al., MoCoGAN: Decomposing Motion and Content for Video Generation
– Tian et al., A Good Image Generator Is What You Need For High-Resolution Video Synthesis
– Sexena et al., Clockwork Variational Autoencoders
– Villegas et al., Stochastic Residual Video Prediction
– Lee et al., Revisiting Hierarchical Approach for Persistent Long-Term Video Prediction
④ Discrete representation
– Yan et al., VideoGPT: Video Generation using VQ-VAE and Transformers
– Wu et al., NÜWA: Visual Synthesis Pre-training for Neural visUal World creAtion
⑤ Continuous-time models
– Skorokhodov et al, StyleGAN-V: A Continuous Video Generator with the Price, Image Quality and Perks of StyleGAN2
Lecture#6 그래프 데이터를 위한 신경망 모형과 응용, 김동우 교수, POSTECH
GNN : Graph Neural Network
목적 : Neural Network 를 통해서 그래프를 학습 시킴.
Naive Approach
=> concatenate adjacent matrix and feature vector
문제점
– parameter 개수가 그래프 Size 에 비례
– graph node 개수가 다르면 재활용 불가
– 인접 행렬 Node 가 reordering 가능하지 않음
GNN : node embedding ( vector representation )
Design a Graph Encoder
– Basic Idea : see neighbor nodes
– Recursive -> Tree Structure
– Two steps :
① Aggregation ( Mean, …)
② Combine ( FC layers, … )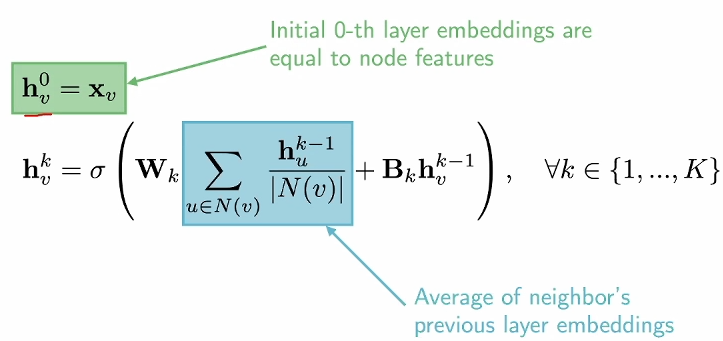
In Practice,
Z = \tilde{D}^{-\dfrac{1}{2}} \tilde{A} \tilde{D}^{-\dfrac{1}{2}} X W\tilde{A} = A + I_N
Node 들의 Embedding 산출 Mechanism => Inductive Capability 로 연결 됨.
– 관찰되지 않은 그래프에 대해서 Embedding 산출 가능
Unsupervised Approach
– “similar” nodes have similar embeddings
Node Level Tasks
– Attribute Masking / Edge prediction / Context prediction
Representation Power of GNN
– graph isomorphism test -> injectivity
Mean pooling / Max pooling are not injective
Injective Multi-set Function
\phi(\sum_{x \in S} f(x))– sum pooling
– total pairwise squared distance
Adversarial attacks on GNN
2022.2.18
Lecture#7 Recent Advances in Text-to-Image Generation Models, 김세훈 박사, Kakao Brain
Auto Regressive Image Generation
Oord et al, Pixel Recurrent Neural Networks, ICML 2016
Salimans et al, PIXELCNN++: IMPROVING THE PIXELCNN WITH DISCRETIZED LOGISTIC MIXTURE LIKELIHOOD AND OTHER MODIFICATIONS, ICLR 2017
VQ(Vector Quantization)- VAE
Oord et al, Neural Discrete Representation Learning, NIPS 2017
DALL-E
Ramesh, Zero-Shot Text-to-Image Generation, ICML 2021
Image-Text Pair Datasets
MSCOCO / CC3M / CC12M / WIT / CLIP / ALIGN
VQ-GAN
Esser, Taming Transformers for High-Resolution Image Synthesis, CVPR 2021
Diffusion-based Model
DDPM
Jonathan Ho et al, Denoising diffusion probabilistic models, NIPS 2020
GLIDE
Nichol et al, GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models, arXiv 2021
Their Approach (Kakao)
– minDALL-E ; VQGAN + Transformer 1D
– RQ-VAE ; Residual-Quantized VAE
Lecture#8 Contrastive Learning: Backgrounds, theory and video applications, 김은솔 교수, 한양대
Representation Learning
Pre-training, Fine-tuning, Zero-shot Learning
[NeurIPS 2021 Tutorial] Self-Supervised Learning: Self-prediction and Contrastive Learning
– Self-prediction & Contrastive
Self-prediction : “intra-sample” prediction
Contrastive : “inter-sample” prediction
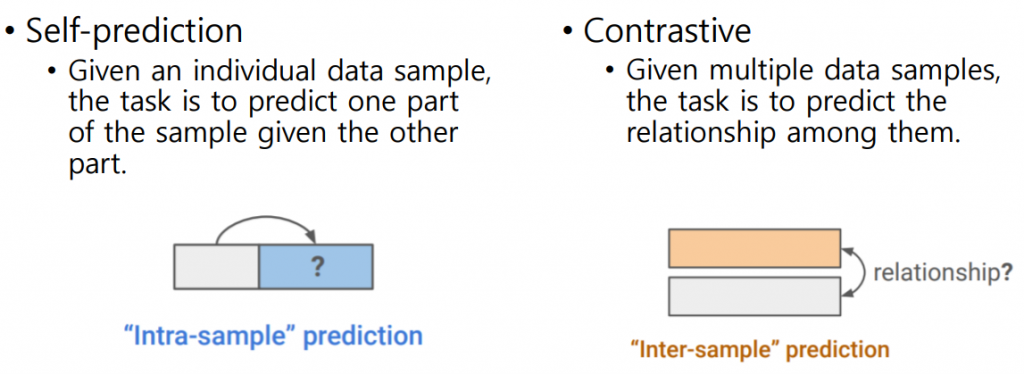
Self-prediction
– Auto-regressive prediction : WaveNet, GPT, PixelRNN, PixelCNN
– Masked Generation
> Early Work : Word2Vec, CBOW & Skip-gram
> BERT
> Vision Transformer
Contrastive
– 비슷한 데이터들은 feature space 상에서 가깝게 하고 상관없는 데이터들은 feature space 상에서 멀게 한다는 매우 간단한 아이디어!

– Early Work
> Hadsell et al, Dimensionality Reduction by Learning an Invariant Mapping, CVPR 2006
( Contrast Loss 최초 제안 )
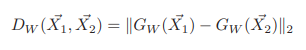
> Triplet Loss, Schroff et al, FaceNet: A Unified Embedding for Face Recognition and Clustering, CVPR 2015
> Lifted Structured Embedding
– MOCO : KaimingHe et al, Momentum Contrast for Unsupervised Visual Representation Learning, CVPR 2020
– SimCLR : Chen et al, A Simple Framework for Contrastive Learning of Visual Representations, ICML 2020
Training with Negative Samples are very important !!!
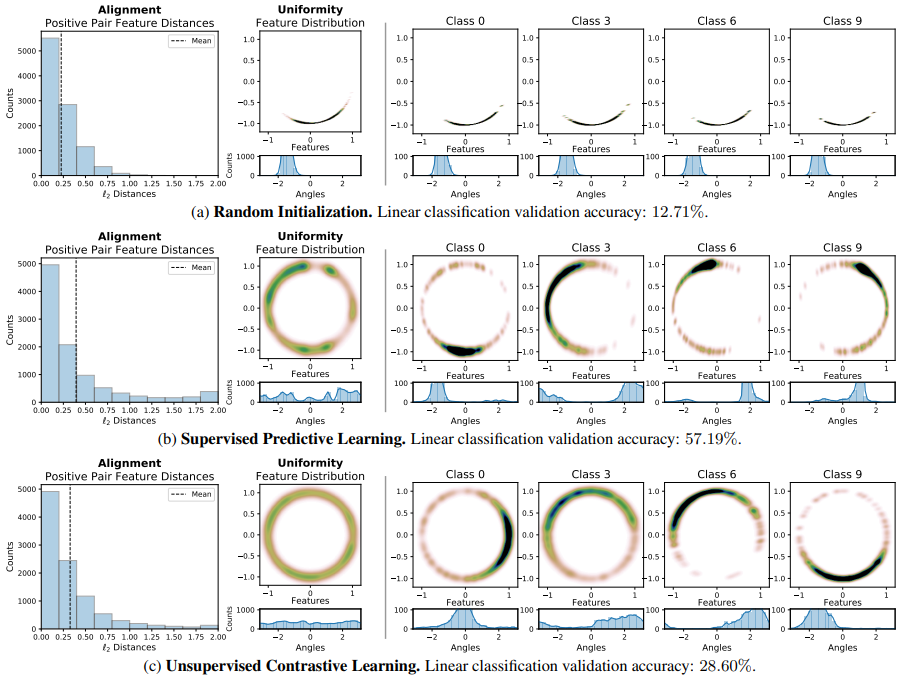
Wang et al, Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere, ICML 2020

Video Representation Learning
비디오 데이터는 데이터 마다 특징이 확연히 다르다. 학습 목표에 따른 적합한 데이터 인지가 중요
– Youtube 8M Challenge
> Input : Image 1024 dim, Audio 128 dim
> Sequence : 230.2 sec
> Output : Multi-Label Class labels
> Data : 6.1M clips / 1.53 TB
– Video Datasets
> One Action with Simple Text
– Kinetics 400/600/700
– UCF 101
> Several Actions with Few Descriptions
– Something-Something
– FineGym
> Long and Multimodal
– Youtube 8M
– HowTo100M
Video Representation Learning with Transformers
- Sun et al, VideoBERT: A Joint Model for Video and Language Representation Learning, ICCV 2019
- Sun et al, Learning Video Representations using Contrastive Bidirectional Transformer, arXiv 2019
- Miech et al, End-to-End Learning of Visual Representations from Uncurated Instructional Videos, CVPR 2020
- Luo et al, UniVL: A Unified Video and Language Pre-Training Model for Multimodal Understanding and Generation, arXiv 2020