이번 포스트는 χ2, t, F 표본 분포 (Sampling Distribution related to the normal Distribution) 을 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다. 이 책의 정리 7.3과 정의 7.2, 정의 7.3 을 다룬다.
1. χ2 표본 분포
\chi^2 분포는 많은 추론 절차에서 중요한 역할을 한다. 예를들어, 정규 모집단으로부터 랜덤 표본 Y_1,Y_2,...,Y_n 을 기초로한 모분산 σ2 를 추론하고자 한다고 보자. 추청 포스트에서 확인한 것과 같이 σ2에 대한 좋은 추정량은 표분 분산
S^2=\dfrac{1}{n-1}\displaystyle\sum^{n}_{i=1}(Y_i-\bar{Y})^2
이 된다. 다음 정리를 통해 S2 통계량의 함수의 확률 분포 제시한다.
| 정리 7.3
Y_1,Y_2,...,Y_n 를 평균 μ와 분산 σ2 를 갖는 정규 분포로부터 추출된 랜덤 표본이라고 하자. 그러면 \dfrac{(n-1)S^2}{\sigma^2} = \dfrac{1}{\sigma^2}\displaystyle\sum^{n}_{i=1}(Y_i-\bar{Y})^2
는 (n-1) 자유도를 갖는 \chi^2 분포를 갖는다. 또한 \bar{Y} 와 S^2 는 독립 랜덤 변수이다.
증명. 일반적인 n 에 대한 증명은 미루고, n=2 인 경우를 생각해 보자. n=2 인 경우에, \bar{Y}=(1/2)(Y_1+Y_2) 이고 따라서, S^2=\dfrac{1}{2-1}\displaystyle\sum^{2}_{i=1}(Yi-\bar{Y})^2=\Big[Y1-\dfrac{1}{2}(Y_1+Y_2)\Big]^2+\Big[Y2-\dfrac{1}{2}(Y_1+Y_2)\Big]^2 =\Big[\dfrac{1}{2}(Y_1-Y_2)\Big]^2+\Big[\dfrac{1}{2}(Y_2-Y_1)\Big]^2 =2\Big[\dfrac{1}{2}(Y_1-Y_2)\Big]^2=\dfrac{(Y_1-Y_2)^2}{2}
따라서, n=2 일때, \dfrac{(n-1)S^2}{\sigma^2}=\dfrac{(Y_1-Y_2)^2}{2\sigma^2}=\Big(\dfrac{Y_1-Y_2}{\sqrt{2\sigma^2}}\Big)^2
우리는 이 양이 표준 정규 랜덤 변수의 제곱(Z2)이라는 것을 보일 것이다. ( 특별히 Z2 은 자유도 1인 \chi^2 분포를 가진 다. ) Y_1-Y_2 는 독립적인 정규 분포의 랜덤 변수의 선형 결합이다. ( Y_1-Y_2=a_1Y_1+a_2Y_2, ~~a_1=1 ~and~ a_2=-1 ) Y_1-Y_2 는 평균 1\mu-1\mu=0 와 분산 (1)^2\sigma^2+(-1)^2\sigma^2=2\sigma^2 인 정규 분포를 갖는다. 그러므로, Z=\dfrac{Y_1-Y_2}{\sqrt{2\sigma^2}}
는 표준 정규 분포를 갖는다. n=2 이기 때문에, \dfrac{(n-1)S^2}{\sigma^2}=\Big(\dfrac{Y_1-Y_2}{\sqrt{2\sigma^2}}\Big)^2=Z^2
은 (n-1)S^2/\sigma^2 는 자유도 1인 \chi^2 분포를 갖는다. |
2. t 표본 분포
이전 포스트에서 정리 7.1은 알려진 분산 σ2 을 갖는 정규 모집단의 평균 μ 에 대한 추론 방법에 대한 기초를 제공해 준다. 정리 7.1은 \sqrt{n}(\bar{Y}-\mu)/\sigma 는 표준 정규분포를 갖는다는 것을 말해준다. σ이 미지일 때, 이것은 S=\sqrt{S^2} 으로 추정가능하고,
\sqrt{n}\Big(\dfrac{\bar{Y}-\mu}{S}\Big)
는 μ에 대한 추론 방식을 제공한다. 우리는 \sqrt{n}(\bar{Y}-\mu)/\sigma 가 n-1 자유도의 Student’s t 분포를 갖는다는 것을 증명할 것이다. 일반적인 Student’s t 분포 (또는 간단히 t 분포) 를 갖는 랜덤 변수의 정의는 다음과 같다.
| 정의 7.2
Z 를 표준 정규 랜덤 변수라고하고, W 를 \nu 자유도의 \chi^2 분포의 변수라고 하자. 그러면, Z 와 W 가 독립이라면, T =\dfrac{Z}{\sqrt{W/\nu}}
는 \nu 자유도 (degree of freedom, d.f.) 의 t 분포를 갖는다고 한다. |
Y_1,Y_2,...,Y_n 가 평균 μ 와 분산 σ2 의 정규 모집단으로부터 추출된 표본이라고하면, 정리7.1 로 Z = \sqrt{n}(\bar{y}-\mu)/\sigma 가 표준 정규 분포를 갖는다는 걸 보일 수 있다. 정리 7.3 은 W = (n-1)S^2/\sigma^2 가 \nu = n-1 자유도의 \chi^2 분포를 갖고, Z 와 W 가 독립 ( \bar{Y} 와 S^2 이 서로 독립이기 때문에) 이라는 것을 말해준다. 정의 7.2에 의해서
T = \dfrac{Z}{\sqrt{W/\nu}}=\dfrac{\sqrt{n}(\bar{Y}-\mu)/\sigma}{\sqrt{[(n-1)S^2/\sigma^2]/(n-1)}}=\sqrt{n}\Big(\dfrac{\bar{Y}-\mu}{S}\Big)
는 (n-1) 자유도의 t 분포를 갖는다.
t 밀도 함수의 식은 여기서 나오진 않는다. 표준 정규 밀도 함수와 마찬가지로, t 밀도 함수는 0을 기준으로 대칭이다. 또한 \nu > 1 일 때, E(T)=0 이고, \nu > 2 일 때, V(T) = \nu/(\nu-2) 이다. 따라서 t 분포의 랜덤 변수는 표준 정규 분포와 같은 기대값을 갖는 것을 알 수 있다. 하지만 표준 정규 분포는 항상 분산이 1이다. 반면에 t 분포를 갖는 변수의 분산은 항상 1을 초과한다.
표준 정규밀도 함수와 t 밀도 함수는 아래 그림에 표현되었다. 두 밀도 함수는 중심으로부터 대칭이다. 하지만 t 분포가 꼬리 쪽에서 밀도가 더 높다.
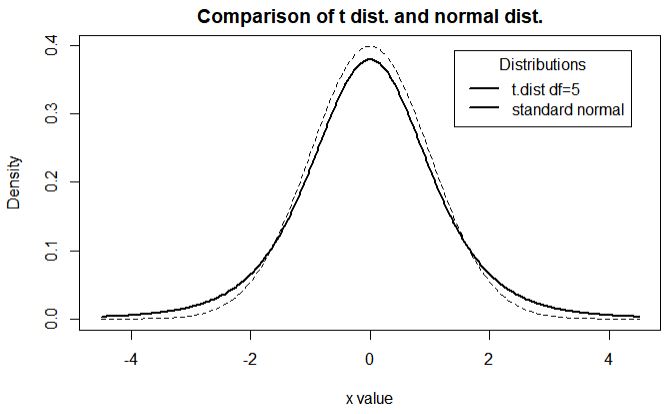
P(T>t_{\alpha}) = \alpha~for~\alpha=0.100, 0.050, 0.025, 0.010, 0.005 를 만족하는 t_{\alpha} 는 t 분포표에 제공된다.
| 예제1.
어떤 철사의 인장력이 미지의 평균값 μ와 미지의 분산값 σ2의 정규 분포를 갖는다고 한다. 여섯 가닥의 철사가 큰 roll 에서 선택되었고, Yi 가 각 측정치 i=1,2,...,6 의 장력이라고 한다. 모집단 평균 μ 와 분산 σ2 은 \bar{y} 와 S^2 로 각각 추정할 수 있다. \sigma^2_{\bar{Y}}=\sigma^2/n 이기 때문에 \sigma^2_{\bar{Y}} 은 S^2/n 으로 추정가능하다. 모 평균 μ 과 2S/\sqrt{n} 내에 \bar{Y} 가 포함되는 확률을 구하라. |
풀이.
우리는 다음을 구하고자 한다.
P \Bigg[-\dfrac{2S}{\sqrt{n}} \leq (\bar{Y}-\mu) \leq \dfrac{2S}{\sqrt{n}}\Bigg] = P\Bigg[-2 \leq \sqrt{n}\Big(\dfrac{\bar{Y}-\mu}{S}\Big) \leq 2 \Bigg]=P(-2 \leq T \leq 2)
( T 는 n-1 =5 자유도를 갖는 t 분포를 갖는다. ) t 분포표에서 2.015 오른쪽 꼬리 영역의 확률이 0.05 인걸 알 수 있기 때문에,
P(-2.015 \leq T \leq 2.015)=0.90
그리고 \bar{Y} 가 μ의 추정된 표준편차의 2배 안에 들어올 확률(within two estimated standard deviations of μ) 은 0.90 이 된다.
만약, σ2 이 알려져 있다면 \bar{Y} 가 μ의 2\sigma_{\bar{Y}} 내에 들어올 확률은
P\Big[-2\Big(\dfrac{\sigma}{\sqrt{n}}\Big) \leq (\bar{Y}-\mu) \leq 2\Big(\dfrac{\sigma}{\sqrt{n}}\Big)\Big]=P\Big[-2 \leq\sqrt{n}\Big(\dfrac{\bar{y}-\mu}{\sigma}\Big) \leq 2\Big]=P(-2\leq Z\leq2)=0.9544
3. F 표본 분포
두 모집단으로부터 얻어진 독립적인 랜덤 표본으로부터 두 정규 모집단의 분산을 비교하고 싶다고 하자. 두 모집단으로부터 크기 n_1 , n_2 인 표본들이 추출되었고, 모집단의 분산은 각각 \sigma^2_1 , \sigma^2_2 이라고 하자. 만약 표본 1로부터 표본 분산 S^2_1 를 계산하고, 표본 2로부터 S^2_2 을 계산한다면, S^2_1 , S^2_2 은 각각 \sigma^2_1 , \sigma^2_2 을 추정한다. 따라서 직관적으로 비율 S^2_1 / S^2_2 는 \sigma^2_1 과 \sigma^2_2 의 상대적 크기를 추론하는데 사용할 수 있을 것이다. 만약 S^2_i 를 \sigma^2_i 로 나누면 결과 비율은,
\dfrac{S^2_1/\sigma^2_1}{S^2_2/\sigma^2_2} = \Bigg(\dfrac{\sigma^2_2}{\sigma^2_1}\Bigg)\Bigg(\dfrac{S^2_1}{S^2_2}\Bigg)
는 분자 자유도 ( n_1-1 ) 와 분모 자유도 ( n_2-1 ) 를 갖는 F 분포를 갖는다. F 분포를 갖는 랜덤 변수의 일반적인 정의는 다음과 같다.
| 정의 7.3
W_1 과 W_2 를 독립적인 \chi^2 분포의 자유도 \nu_1 과 \nu_2 의 랜덤 변수라고 하자. 그러면, F = \dfrac{W_1/\nu_1}{W_2/\nu_2}
는 분자 자유도 \nu_1 과 분모 자유도 \nu_2 의 F 분포를 갖는다고 말한다. |
F 가 분자 자유도 \nu_1 과 분모 자유도 \nu_2 의 F 분포를 갖으면, E(F)=\nu_2/(\nu_2-2) if \nu_2>2 이고 V(F) = [2\nu^2_2(\nu_1+\nu_2-2)]/[\nu_1(\nu_2-2)^2(\nu_2-4)] 임을 보일 수 있다. F 분포의 평균은 오직 분모의 자유도 \nu_2 에만 의존한다는 것에 주목하라.
다시 정규 분포로부터 추출된 독립적인 랜덤 표본들에 대해 생각해 보자. 우리는 W_1=(n_1-1)S^2_1/\sigma^2_1 과 W_2=(n_2-1)S^2_2/\sigma^2_2 이 각각 자유도 \nu_1 =(n_1-1) 과 \nu_2 =(n_2-1) 의 \chi^2 분포를 갖는 다는 것을 알고 있다. 정의 7.3 을 통해서,
F = \dfrac{W_1/\nu_1}{W_2/\nu_2}=\dfrac{[(n_1-1)S^2_1/\sigma^2_1]/(n_1-1)}{[(n_2-1)S^2_2/\sigma^2_2]/(n_2-1)}=\dfrac{S^2_1/\sigma^2_1}{S^2_2/\sigma^2_2}
는 분자 자유도 (n_1-1) 과 분모 자유도 (n_2-1) 의 F 분포를 갖는다.
일반적인 F 분포가 아래 그림에 나타냈다. P(F >F_{\alpha}) = \alpha 를 만족하는 F_{\alpha} 는 F 분포표에 제공된다.
