- 가설검정 (Hypothesis Testing) – 통계적 검정의 요소
- 가설검정 (Hypothesis Testing) – 다(多) 표본 검정
- 가설검정 (Hypothesis Testing) – Type Ⅱ Error 확률 계산과 Z-Test Sample Size 찾기
- 가설검정 (Hypothesis Testing) – 가설검정절차와 신뢰구간사이의 관계
- 가설검정 (Hypothesis Testing) – 통계 검정 결과를 보고하는 다른 방법: 유의수준 또는 p-value
- 가설검정 (Hypothesis Testing) – 가설 검정의 이론에 대한 추가 설명
- 가설검정 (Hypothesis Testing) – 소(小) 표본 가설검정; μ 그리고 μ1 – μ2
- 가설검정 (Hypothesis Testing) – 분산에 관련된 가설검정
이번 포스트는 가설검정의 여덟 번째 포스트로 분산에 관련된 가설검정 (Testing Hypothesis Concerning Variances) 를 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.
8. 분산에 관련된 가설검정 (Testing Hypothesis Concerning Variances)
우리는 다시 한번, Y_1, Y_2, ... , Y_n 를 모 평균 μ 와 모 분산 σ2 을 모르는 정규분포로부터의 크기 n 인 랜덤 샘플이라고 가정하자. 추정-9번째 포스트에서 파라미터 \sigma^2 의 신뢰구간을 형성하기 위한 pivotal 방법을 사용했다. 이번 장에서는 고정된 \sigma^2_0 에 대해 귀무가설 H_0~:~\sigma^2=\sigma^2_0 를 검정하는 문제를 다루고자 한다. 만약 H_0 가 참이고, \sigma^2 = \sigma^2_0 이면, 정리 7.3 에 의해
\chi^2 = \dfrac{(n-1)S^2}{\sigma^2_0}
는 자유도 n-1인 \chi^2 분포를 따른다. 만약 우리가 귀무가설 H_0~:~\sigma^2=\sigma^2_0 와 대립가설 H_a~:~\sigma^2>\sigma^2_0 을 검정하고 싶다면 \chi^2 =(n-1)S^2/{\sigma^2_0} 를 검정통계량으로 사용할 수 있다. 하지만 기각역 (rejection region) 은 어떻게 설정할 것인가?
만약 대립가설 H_a 가 참이고 실제 \sigma^2 가 \sigma^2_0 보다 크다면, S^2 (실제 \sigma^2 를 추정하는 값) 은 \sigma^2_0 보다 커야 한다. \sigma^2_0 에 비해 큰 S^2 은 대립가설 H_a~:~\sigma^2>\sigma^2_0 을 지지하는 강력한 근거가 된다. S^2 이 \sigma^2_0 에 비해 크다는 것과, \chi^2 =(n-1)S^2/{\sigma^2_0} 이 크다는 것은 동치임을 주지하기 바란다. 따라서 어떤 상수 값 k 에 대하여 기각역 RR=\{\chi^2>k\} 은 귀무가설 H_0~:~\sigma^2=\sigma^2_0 와 대립가설 H_a~:~\sigma^2>\sigma^2_0 를 검정하는데 적합하게 사용될 수 있다. 만약 type I error 의 확률 \alpha 가 주어졌다면, 기각역은
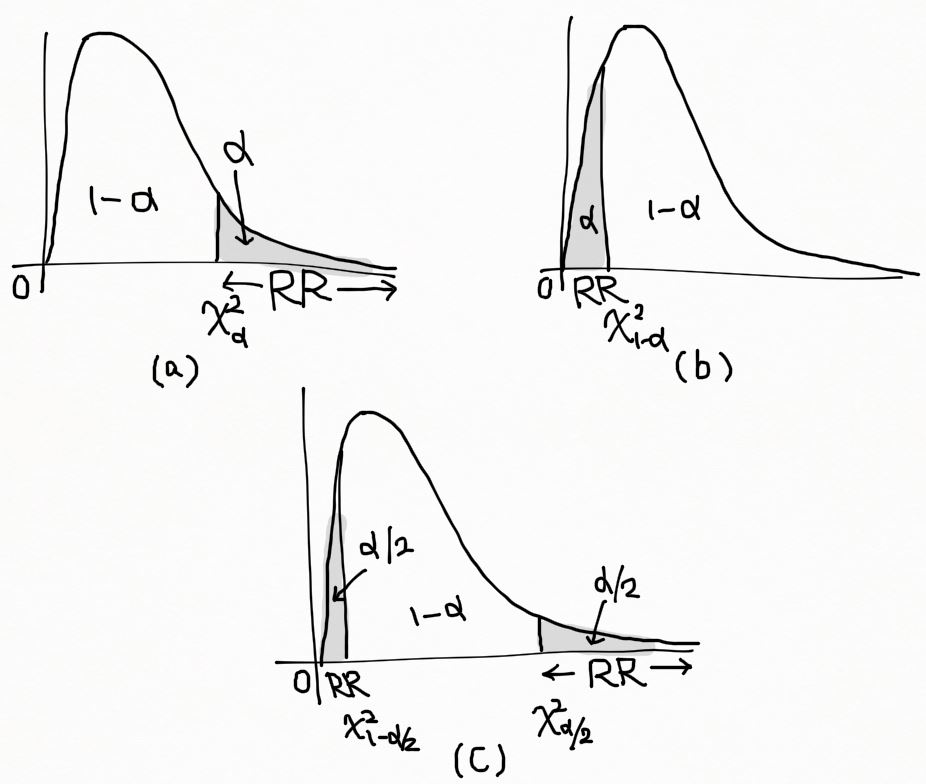
P(\chi^2>\chi^2_{\alpha})=\alpha 인 RR=\{\chi^2>\chi^2_{\alpha}\} 이 된다. (아래 그림 (a) 에 표시)
만약 귀무가설 H_0~:~\sigma^2=\sigma^2_0 와 대립가설 H_a~:~\sigma^2<\sigma^2_0 (lower tail alternative) 는 마찬가지로 \chi^2 분포의 lower tail 에 기각역이 위치하며, 한편으로 귀무가설 H_0~:~\sigma^2=\sigma^2_0 와 대립가설 H_a~:~\sigma^2\not=\sigma^2_0 (a two-tailed test) 는 양측 꼬리에 기각역이 위치한다. 이들 기각역은 아래 그림 (b), (c) 에 표시하였다.
| 모집단 분산과 관련된 가설 검정
가정 : Y_1, Y_2, ... , Y_n 가 E(Y_i)=\mu 이고 V(Y_i)=\sigma^2 를 따르는 정규 분포로부터의 하나의 랜덤 표본을 이룬다. H_0~:~\sigma^2 =\sigma^2_0H_a~:\begin{cases} \sigma^2>\sigma^2_0~~~~(upper~tail~alternative) \\\sigma^2<\sigma^2_0~~~~(lower~tail~alternative) \\\sigma^2\not=\sigma^2_0~~~~(two~tailed~alternative) \end{cases}
검정통계량 : \chi^2 = \dfrac{(n-1)S^2}{\sigma^2_0}
기각역 : \begin{cases} \chi^2>\chi^2_{\alpha}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(upper~tail~RR) \\\chi^2<\chi^2_{1-\alpha}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(lower~tail~RR) \\\chi^2>\chi^2_{\alpha/2}~or~\chi^2<\chi^2_{1-\alpha/2}~~~~~~(two~tailed~RR)\end{cases}
자유도 \nu=n-1 인 \chi^2_{\alpha} 값은 P(\chi^2>\chi^2_{\alpha})=\alpha 를 만족한다. |
| 예제1.
공장에서 기계 가공된 엔진 부품의 직경의 분산이 0.0002 보다 크지 않다고 한다. 어떤 크기가 10인 랜덤 표본의 표본 분산은 0.0003 으로 관찰 되었을 때 5% 수준으로 H_0~:~\sigma^2=0.0002 와 H_a~:~\sigma^2>0.0002 를 검정하라. |
풀이.
관찰된 직경은 정규분포를 따른다고 가정하는게 합리적이라면, 적합한 검정 통계량은 \chi^2 =(n-1)S^2/{\sigma^2_0} 이 된다. upper tail test 를 해야 하므로, 검정 통계량 값이 \chi^2_{0.05}=16.919 (자유도는 9) 보다 크면 귀무가설 H0 를 기각할 수 있다. 관측된 값으로 계산하면
\dfrac{(n-1)S^2}{\sigma^2_0}=\dfrac{(9)(0.0003)}{0.0002}=13.5 가 된다.
즉, H0 는 기각할 수 없다. 5% 유의수준에서 모 분산 \sigma^2 가 0.0002 보다 크다는 충분한 근거가 없기 때문이다.
| 예제2.
예제1. 의 p-value 를 결정하라. |
풀이.
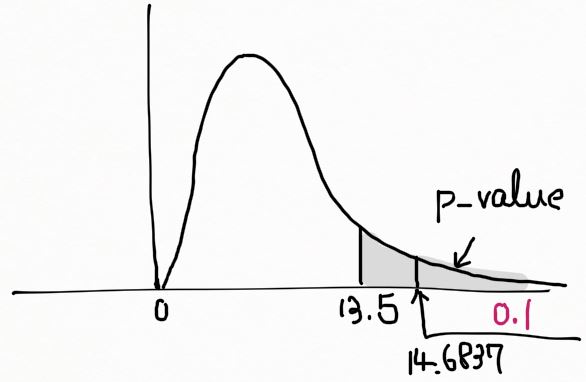
자유도 9인 \chi^2 분포에서 13.5 보다 큰 확률 값이 p-value 가 된다. \chi^2_{0.1}=14.6837 이며, 아래 그림에서 빗금친 영역은 0.1을 넘어선다. 따라서 p-value > 0.1
즉, 귀무가설은 기각되지 못한다.
| 예제3.
어떤 실험자가 계측기의 표준편차가 2.0 이라고 확신한다고 한다. 16번의 계측에서 s^2 =6 이 관찰 되었다면, 이들 데이터가 그의 주장을 뒷받침하는 것인가? 검정의 p-value 도 결정하라. 만약 α = 0.05 로 선택한다면 어떤 결론을 내릴 것인가? |
풀이.
우리는 귀무가설 H_0~:~\sigma^2=4 와 H_a~:~\sigma^2\not=4 , 즉 two-tailed test 를 수행해야 한다. 검정통계량 값은 \chi^2=15(6.1)/4 = 22.875 이다. 자유도 15를 갖는 경우 \chi^2_{0.05}=24.9958 이고, \chi^2_{0.10}=22.3072 이므로 p-value 는 0.05 와 0.1 사이에 위치한다. 우리는 lower-tail 쪽 역시 검정해야 하므로 (마찬가지로 0.05 에서 0.1 사이) 0.1 < p-value < 0.2 가 된다. 따라서 선택한 α = 0.05 는 가장 작은 p-value 보다도 작기 때문에 우리는 귀무가설을 기각할 수 없다.
때로 우리는 두 정규분포간의 분산을 비교하고 싶다. 특별히 그 둘의 분산이 같은지 비교하고 싶을 때가 있다. 이런 문제들은 두 계측 기구의 정확성을 비교하거나 제조된 제품의 품질 특성의 산포를 비교할 때, 두 검정 절차의 스코어의 분포를 비교할 때 등이다. 예를들어, Y_{11}, Y_{12}, ... , Y_{1n_1} 와 Y_{21}, Y_{22}, ... , Y_{2n_2} 를 모 평균을 모르고 V(Y_{1i})=\sigma^2_1 이고, V(Y_{2i})=\sigma^2_2 인 정규 분포로부터 구해진 독립적인 랜덤 표본이라고 하자. ( \sigma^2_1 과 \sigma^2_2 는 미상). 우리는 귀무가설 H_0~:~\sigma^2_1 = \sigma^2_2 에 대한 대립가설 H_a~:~\sigma^2_1 > \sigma^2_2 를 검정하고자 한다.
표본 분산인 S^2_1 과 S^2_2 은 각 모집단의 분산인 \sigma^2_1 과 \sigma^2_2 을 추정하므로, 만약 S^2_1 이 S^2_2 에 비해 매우 크다면 대립가설 Ha 를 지지하고 귀무가설 H0 를 기각할 수 있다. 즉, 우리는 기각역 RR 을 아래와 같이 쓸 수 있다.
RR = \{\dfrac{S^2_1}{S^2_2}>k \}
여기서 k 는 type I error 의 확률이 α 가 되도록 선택할 수 있다. 적합한 k 값은 통계량 S^2_1/S^2_2 의 확률분포를 따르게 된다. (n_1-1)S^2_1 /\sigma^2_1 과 (n_2-1)S^2_2 /\sigma^2_2 은 독립적인 chi-square 랜덤 변수임을 주지하기 바란다. 정의 7.3 에 따라,
F = \dfrac{(n_1-1)S^2_1}{\sigma^2_1(n_1-1} / \dfrac{(n_2-1)S^2_2}{\sigma^2_2(n_2-1)} = \dfrac{S^2_1\sigma^2_2}{S^2_2\sigma^2_1}
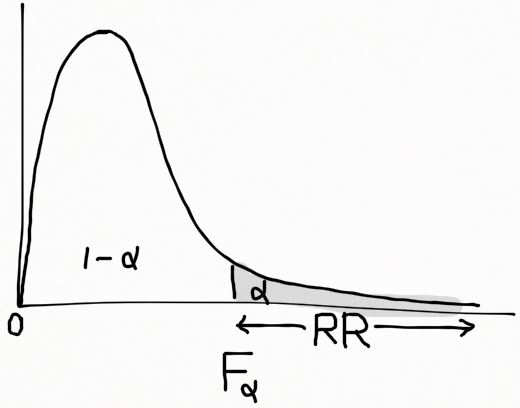
는 분자의 자유도 (n_1-1) 와 분모의 자유도 (n_2-1) 를 따른다. 귀무가설 \sigma^2_1 = \sigma^2_2 하에서는 F = S^2_1/S^2_2 이고, k= F_{\alpha} 일 때, 기각역 RR =\{F>k\}=\{F>F_{\alpha}\} 와 같다. 즉, 분자와 분모의 자유도가 \nu_1=(n_1-1) 와 \nu_2=(n_2-1) 이고, P(F>F_{\alpha})=\alpha 를 말한다. 기각역은 아래 그림에 표현하였다.
| 예제 4.
우리는 부품 직경에 대한 산포를 경재사의 부품의 직경과 비교하고 싶어한다. 우리 회사의 표본 분산은 표본크기 10 일 때, s^2_1=0.0003 이고 경쟁사의 표본분산은 표본 크기가 20일 때, s^2_2=0.0001 로 관찰되었다. 이 관찰 결과가 경쟁사의 분산이 더 작다는 근거를 제시해 주는지 α = 0.05 로 검정하라. |
풀이.
귀무가설 H_0~:~\sigma^2_1=\sigma^2_2 에 대한 대립가설 H_a~:~\sigma^2_1>\sigma^2_2 을 검정해야 한다. 검정 통계량은 F = (S^2_1/S^2_2) 이고, 분자 자유도 \nu_1 = 9 이고 분모 자유도 \nu_2 = 19 이다. F_{0.05}=2.42 보다 F 가 크면 귀무가설 H0 를 기각하게 된다. 관측된 결과로부터 검정 통계량은
F = \dfrac{s^2_1}{s^2_2} = \dfrac{0.0003}{0.0001} = 3이 되고, F > F_{0.05} 이므로, 귀무가설 H_0~:~\sigma^2_1=\sigma^2_2 를 기각하고, 대립가설 H_a~:~\sigma^2_1>\sigma^2_2 을 지지할 수 있게 된다. 따라서 경쟁사에서는 직경의 분산(산포)이 더 적게 부품이 제조되고 있다고 결론 내릴 수 있다.
| 예제 5.
예제 4. 의 p-value 를 결정하라. |
풀이.
upper-tail test 로 계산된 F값은 3. 이었다. 해당 값은 분자 자유도 \nu_1 = 9 이고 분모 자유도 \nu_2 = 19 에 기초한 것이므로 F 분포표에서 F_{0.025} = 2.88 이고, F_{0.01}=3.52 이므로 0.01 < p-value < 0.025 라고 할 수 있다.
위 예제4. 에서 대립가설을 H_a~:~\sigma^2_1<\sigma^2_2 로 바꿔보자. 어떻게 진행해야 하는가? 우리는 두 모집단 중 하나를 모집단 “1” 로 지정할 수 있다. 따라서, 두 모집단의 라벨(labels) 을 임의로 변경한다면 (그리고 해당하는 표본 크기와 표본 분산도 바꾼다면), 대립가설은 H_a~:~\sigma^2_1>\sigma^2_2 이 된다. 이전과 마찬가지로 진행할 수 있다. 즉, 한 모집단의 분산이 다른 모집단의 분산보다 크다는 가설을 갖고 있다면, “가설로 세운” 더 큰 분산을 갖는 모집단을 “모집단1” 로 지정하고 진행하면 된다.
| H_a~:~\sigma^2_1=\sigma^2_2 가설 검정
가정 : 정규 모집단으로부터의 독립 표본 H_0~:~\sigma^2_1=\sigma^2_2H_a~:~\sigma^2_1>\sigma^2_2
검정 통계량 : F = \dfrac{S^2_1}{S^2_2}
기각역 : F>F_{\alpha} , (분자와 분모의 자유도가 \nu_1=(n_1-1) 와 \nu_2=(n_2-1) 이고, P(F>F_{\alpha})=\alpha 를 만족할 때) |
만약, 귀무가설 H_0~:~\sigma^2_1=\sigma^2_2 에 대해, 대립가설 H_a~:~\sigma^2_1\not=\sigma^2_2 을 검정하고 싶다면 (type I error 확률 = α), F = S^2_1/S^2_2 를 검정통계량으로 하고 F 값이 upper tail 과 lower tail 의 α/2 지점에 온다면 대립가설 Ha를 지지하고 H0 를 기각하게 된다. upper tail 의 결정 값은 바로 구할 수 있지만 lower tail 의 결정 값은 어떻게 구할 수 있을까?
F = S^2_1/S^2_2 의 역(inverse)이 F^{-1} = S^2_2/S^2_1 이며 둘 다 F 분포임을 주지하자. 다만 분자와 분모의 자유도는 뒤 바뀐다. F^a_b 를 분자 자유도 a 를 갖고, 분모 자유도 b를 갖는 F 분포를 따르는 랜덤 변수로 정의하자. 그리고 F^a_{b, \alpha/2} 는
P(F^a_b > F^a_{b, \alpha/2}) =\alpha/2
를 만족한다. 그러면,
P[(F^a_b)^{-1} <(F^a_{b, \alpha/2})^{-1}] =\alpha/2
이고, 따라서
P[F^b_a <(F^a_{b, \alpha/2})^{-1}] =\alpha/2
즉, F^b_a 분포의 lower-tail 의 \alpha/2 로 cut-off 되는 값은 F^a_{b, \alpha/2} 를 역산해서 구할 수 있다. 따라서 만약 F = S^2_1/S^2_2 를 귀무가설 H_0~:~\sigma^2_1=\sigma^2_2 에 대해, 대립가설 H_a~:~\sigma^2_1\not=\sigma^2_2 의 검정통계량으로 사용한다면, 적합한 기각역은 다음과 같다.
RR~:~\{F>F^{n_1-1}_{n_2-1, \alpha/2}~or~F<(F^{n_2-1}_{n_1-1, \alpha/2})^{-1}\}
(첫번째 (a, b)에는 (n_1-1,n_2-1) 를, 두번째 (a, b) 에는 (n_2-1,n_1-1) 로 하면 성립하는 것을 확인할 수 있다.)
동일한 검정 방법은 다음과 같다. n_L 와 n_S 각각을 표본분산이 큰 표본 크기와 표본분산이 작은 표본 크기라고 하자. F 통계량에서 더 큰 표본분산을 분자에 놓고, 작은 표본분산을 분모로 한다. 그렇게 하면 F > F_{\alpha/2} 일 때, 귀무가설 H_0~:~\sigma^2_1=\sigma^2_2 을 기각하고, 대립가설 H_a~:~\sigma^2_1\not=\sigma^2_2 을 지지한다. ( 분자의 자유도는 \nu_1 = n_L-1 이고, 분모의 자유도는 \nu_2=n_S-1 이다. )
| 예제 6.
실험자가 전기충격에 대한 남성과 여성의 고통 임계값을 확인하고 있다. 아래 표와 같이 결과가 나왔다면, 남성과 여성 사이에 고통 임계에 대한 산포에 차이가 있다고 할 충분한 근거가 되는지 α = 0.10 으로 검정하라. p-value 는 어떠한가?
|
풀이.
남성과 여성의 고통 임계값은 근사적으로 정규 분포를 따른다고 하자. 우리는 귀무가설 H_0~:~\sigma^2_M=\sigma^2_F 에 대한 대립가설 H_a~:~\sigma^2_M\not =\sigma^2_F 를 테스트하고자 한다. (여기서 \sigma^2_M 은 남성 고통 임계 모 분산이고 \sigma^2_F 는 여성 고통 임계 모 분산이다.) 더 큰 표분 분산 S^2 이 26.4 (여성) 이므로, n_L =10 이고, 작은 표본분산 S^2 이 12.7 (남성) 이므로, n_S =14 이다. 따라서
F = \dfrac{26.4}{12.7} = 2.079
이며, 분자 자유도 \nu_1 = 10-1 = 9 와 분모 자유도 \nu_2 = 14-1 = 13 을 만족하는 F_{\alpha/2}=F_{0.05}=2.71 이다. 검정 통계량 값과 비교해 보면, 2.71 보다 F_{0.05} 가 더 크기 때문에 남성과 여성 사이에 고통 임계 값의 분산에 차이가 있다는 충분한 근거가 부족하다. p-value 는 F_{0.10} = 2.16 이기 때문에 p-value > 2(0.1) = 0.20 이다. 따라서 매우 큰 \alpha 를 사용하지 않으면 남성과 여성 사이에 고통 임계 값 분산에 차이가 있다는 결론에 다다를 수 없다.