추정 (Estimation) – 모분산에 대한 신뢰구간

 

 

 

 

 

이번 포스트는 추정(Estimation) 의 아홉 번째 포스트로 모분산에 대한 신뢰구간 (Confidence Intervals for σ²) 을 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.

 

9. 모분산에 대한 신뢰구간 (Confidence Intervals for σ²)

모분산 σ² 은 모집단의 변동량을 규정한다. 많은 경우에 실험자는 실제 모분산 σ² 을 알 수 없고, 추정해야 한다. 추정-3번째 포스트에서 S^2=[1/(n-1)]\sum^{n}_{i=1}(Y_i-\bar{Y})^2 는 σ² 에 대한 불편 추정량 (unbiased estimator) 라는 것이 증명되었다. μ에 대한 우리의 신뢰구간 형성 과정을 통해서,  σ² 을 알 수 없을 때, S² 이 불편 추정량으로 사용되었다.

\mu 와 \mu_1 -\mu_2 에 대한 신뢰구간을 계산하기 위해서 σ² 에 대한 정보가 필요한 것에 덧붙여서, σ² 에 대한 신뢰구간을 형성하고 싶은 경우가 있을 수 있다. 예를 들어 우리가 어떤 정제약에 대해 화학 조성 분석을 수행하고 싶다면, 정제약의 구성요소들의 평균 조성양과 σ² 로 규정되는 정제약들간의 변동양을 확인해 봐야 한다.

구간 추정 절차를 진행하기 위해서, pivotal 양이 필요하다.  랜덤 표본 Y_1,Y_2,...,Y_n 가 평균 \mu 와 분산 \sigma^2 을 갖는 정규 분포로부터 추출된 표본이라고 하자. 정리 7.3으로부터

\dfrac{\displaystyle\sum^{n}_{i=1}(Y_i-\bar{Y})^2}{\sigma^2}=\dfrac{(n-1)S^2}{\sigma^2}

 

는 (n-1) 자유도를 갖는 \chi^2 분포를 갖는다. pivotal 방식을 통해서 신뢰계수 (1-α) 에 대한

P \Big[ \chi^2_L \leq \dfrac{(n-1)S^2}{\sigma^2} \leq \chi^2_U \Big] = 1-\alpha

 

를 만족하는  \chi^2_L 와  \chi^2_U 를  찾을 수 있다. ( 윗첨자 L 과 U 는 하한, 상한을 각각 뜻한다. )  \chi^2 분포는 대칭적이지 않기 때문에,  \chi^2_L 와  \chi^2_U 을 선택하는 자유도를 갖는다. 우리는 (1-α) 확률로 σ² 을 포함하는 가장 짧은 신뢰구간을 찾고자 한다. 이것은 일반적으로 어렵고, trial-and-error 방법을 통해서 적합한  \chi^2_L 와  \chi^2_U 을 찾아야 한다. 아래 그림에서 표현된 바와 같이, 동일한 꼬리 영역에 대한 지점을 선택할 수 있다.

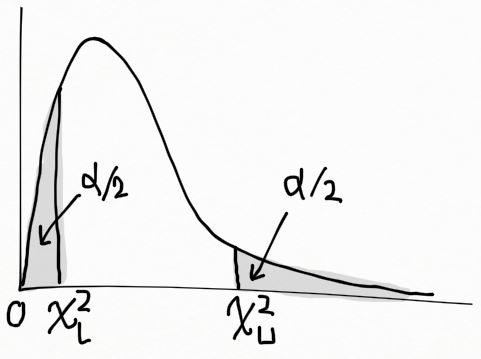
결과로, 아래를 얻는다.

P \Big[\chi^2_{(\alpha/2)} \leq \dfrac{(n-1)S^2}{\sigma^2} \leq \chi^2_{1-(\alpha/2)} \Big]=1-\alpha

 

그리고 부등식을 재배열하면,

P \Big[ \dfrac{(n-1)S^2}{\chi^2_{1-(\alpha/2)}} \leq \sigma^2 \leq  \dfrac{(n-1)S^2}{\chi^2_{(\alpha/2)}} \Big]= 1-\alpha

 

\sigma^2 의 신뢰구간은 다음과 같다.

\sigma^2 에 대한 100(1-\alpha)% \Bigg(\dfrac{(n-1)S^2}{\chi^2_{(\alpha/2)}},\dfrac{(n-1)S^2}{\chi^2_{1-(\alpha/2)}} \Bigg)

 

예제1. 실험자가 소리의 크기를 측정할 수 있는 측정기를 사용하여 얻어진 측정결과의 변동량을 확인하고 싶어한다. 동일한 소리에 대해 이 측정기를 통해 독립적인 3개의 결과가 4.1, 5.2, 10.2 로 나왔다. 0.90의 신뢰계수로 σ2 을 추정하라.

풀이.

이 측정기로 기록된 측정결과들이 정규성을 가정한다면, 신뢰구간을 바로 형성할 수 있다. 측정된 결과로 s^2 = 10.57 이 된다. (n-1)=2 자유도이고 \alpha/2=0.05 이므로, \chi^2_{0.95}=0.103 이고  \chi^2_{0.05}=5.991 을 얻는다. 따라서 σ² 의 90% 신뢰구간은,

 

\Bigg(\dfrac{(n-1)s^2}{\chi^2_{0.05}},\dfrac{(n-1)s^2}{\chi^2_{0.95}} \Bigg) 또는 \Bigg(\dfrac{(2)(10.57)}{5.991}, \dfrac{(2)(10.57)}{0.103} \Bigg) ,

 

그리고 이것은 (3.53, 205.24) 가 된다.

이  σ² 에 대한 구간은 굉장히 넓다. n 이 상당히 작기 때문인 것이 주된 이유이다.

 

추정-8번째 포스트에서 \mu 와 \mu_1 - \mu_2 에 대해 도출된 신뢰구간은 모집단이 정규 분포가 아니더라도 지정한 수준의 신뢰계수를 갖는 다는 것을 알게 되었다. 이와 대조적으로, σ² 에 대한 신뢰구간은 모집단이 정규분포가 아닌 경우에는 지정한 수준과 상당히 다른 신뢰계수를 갖는다.

Series Navigation

<< 추정 (Estimation) – 소(小) 표본 신뢰구간 ; μ 와 μ1 – μ2