Chi-Squared (χ2) distribution
카이 제곱분포 또는 영어로 Chi-Squared distribution 이라 불리는 확률분포는 표준 정규분포 (Standard Normal Distribution) 의 독립변수들을 제곱하여 얻어지는 분포이다. 여기서 카이(χ ; Chi) 는 그리스문자에서 따온 것이다.
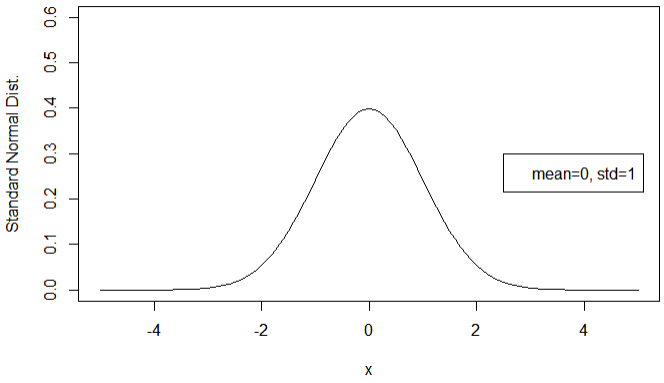
독립변수 X 가 표준정규분포를 따를때,
X \thicksim N(0,1) 처럼 표현하고 아래 그림과 같은 분포를 띈다.
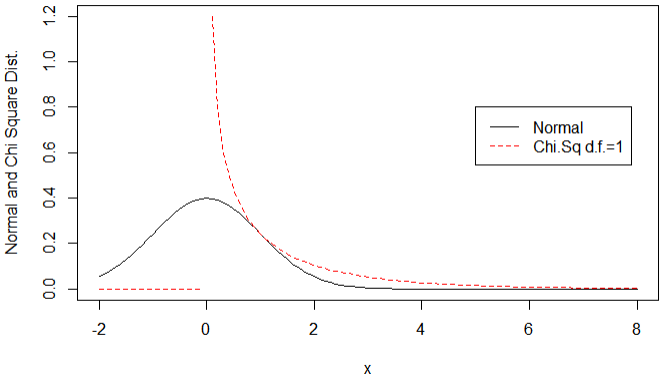
만약 Q_1 가 X^2 처럼 표준정규분포를 따르는 X 의 제곱인 경우, 독립변수 한 개를 사용하므로 degree~of~freedom =1 이 되며,
Q_1 \thicksim \chi^2_1 처럼 표현한다. 아래 첨자는 d.f. (degree of freedom) 를 나타낸다.
표준정규분포의 확률변수를 제곱하게 되므로 당연히 0 이하는 확률이 없고 0이상인 경우만 표현된다. 표준정규분포와 d.f. = 1 인 Chi-Square 분포를 같이 그려서 비교해 보면 아래와 같다.
 만약 Q_2 라는 새로운 확률변수를 X_1^2 + X_2^2 와 같이 두 개의 독립확률변수를 합한 것이라고 하면, d.f. = 2 가 되고 Q_2 \thicksim \chi_2^2 이 된다.
만약 Q_2 라는 새로운 확률변수를 X_1^2 + X_2^2 와 같이 두 개의 독립확률변수를 합한 것이라고 하면, d.f. = 2 가 되고 Q_2 \thicksim \chi_2^2 이 된다.
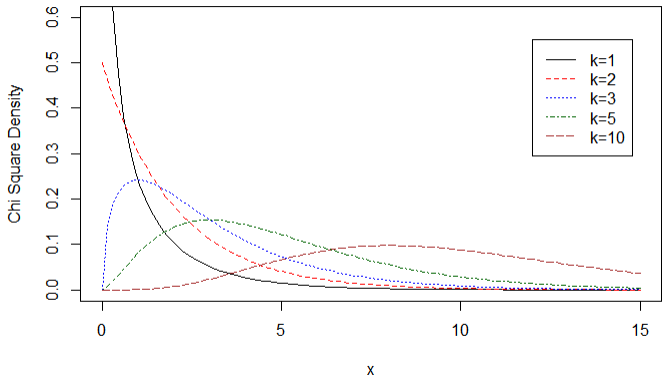
흥미로운 점은 이렇게 제곱하여 더해지는 확률변수가 늘어나게 되면, d.f. 값이 증가하면서 확률분포가 중첩되는 걸 확인할 수 있다는 것이다.
d.f. = 2, 3, 4, … 로 점차 늘려가면서 확률 분포를 비교해 보면 아래와 같이 확률 분포가 변화하는 것을 관찰할 수 있다. d.f. 값이 증가하게 되면서 한쪽으로의 치우침이 사라지고 종 모양의 (bell-shape) 의 그래프를 나타내는데 정규분포와 유사한 형태를 갖게 된다. 실제로 중심극한정리(Central Limit Theorem) 에 의해 n이 무한히 커지면, 카이제곱분포는 정규분포를 따르게 된다.
위 내용은 아래 Khan Academy 의 동영상 강좌를 참고하였고, R plotting 은 여기 를 참고했다. R 소스코드는 GitHub 에 올려두었다.
<Khan Academy 동영상 강좌>