2020 한국인공지능학회 동계강좌 정리 – 4. KAIST 신진우 교수님, Adversarial Robustness of DNN

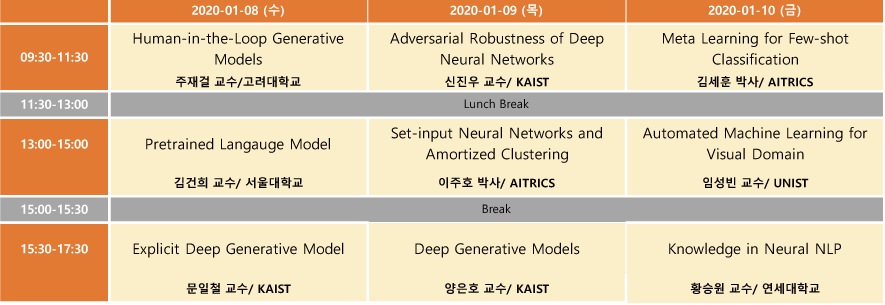
2020 인공지능학회 동계강좌를 신청하여 2020.1.8 ~ 1.10 3일 동안 다녀왔다. 총 9분의 연사가 나오셨는데, 프로그램 일정은 다음과 같다.

전체를 묶어서 하나의 포스트로 작성하려고 했는데, 주제마다 내용이 꽤 많을거 같아, 한 강좌씩 시리즈로 묶어서 작성하게 되었다. 네 번째 포스트에서는 KAIST 신진우 교수님의 “Adversarial Robustness of Deep Neural Networks” 강연 내용을 다룬다.

1. Introduction
   1. What is The Adversarial Example?
      • Problem : ML Systems are highly vulnerable to a small noise on input that are specifically designed by an adversary.
      • Threat of Adversarial Examples
        • Adversarial examples raise issues critical to the “AI safety” in the real world.
        • Adversarial examples exist across various tasks or modalities, ex) segmentation, speech recognition
      • The Adversarial Game : Attacks and Defenses
        • Attacks : Design inputs for a ML system to produce erroneous outputs
        • Defenses : Prevent the misclassification by adversarial examples
        • Threat Model
          1. Adversary goals : simply to cause misclassification or attack into a target class
          2. Adversary capabilities : reasonable constraints to adversary
             • To date, most defenses restrict the adversary to make “small” changes to inputs  d(x, x') < \epsilon
             • a common choice for d(\cdot, \cdot) is l_p distance
          3. Adversary knowledge
             • White-box model : Complete knowledge
             • Black-box model : No knowledge of the model
             • Gray-box : A limited number of queries to the model
      • Evaluating Adversarial Robustness
        • “Adversarial Risk” : The worst-case loss L for a given perturbation budget
          1. E_{(x,y) \sim D}[\max_{x':d(x,x')<\epsilon}L(f(x'), y)]
          2. Objective : Minimize
          3. Cons : one must decide \epsilon
          4. SOTA : FSGM, PGD (explained in later)
        • The average minimum-distance of the adversarial perturbation
          1. E_{(x,y) \sim D}[\min_{x' \in A_{x,y}} d(x, x') ]
          2. Objective : Maximize (Maximize minimum margin)
          3. SOTA : CW (Carlini & Wagner, explained in later )
2. Adversarial Attack Methods
   1. White-box attacks
      • Fast Gradient Sign Method (FGSM)
        • Goodfellow et al, Explaining and Harnessing Adversarial Examples, ICLR 2015
        • Goal : Untargeted Attack, Find argmax_{x':d(x,x')<\epsilon}L(f(x'),y)
        • Capabilities : Pixel-wise restriction :  d(x,x')=\| x-x' \|_{\infty} := \max_i |x_i - x'_i | \leq \epsilon
        • Knowledge : White-box
      • Least-likely Class Method
        • Kurakin et al, Adversarial Machine Learning at Scale, ICLR 2017
        • Goal : Targeted Attack
        • Capabilities : Pixel-wise restriction :  d(x,x')=\| x-x' \|_{\infty} := \max_i |x_i - x'_i | \leq \epsilon
        • Knowledge : White-box
      • Projected Gradient Descent (PGD)
        • Madry et al, Towards Deep Learning Models Resistant to Adversarial Attacks, ICLR 2018
        • \max_{x' \in x + B} L(f(x'), y) , where B is the set of neighbors
        • In some sense, PGD is regarded as the strongest first-order adversary
      • DeepFool
        • Moosavi-Dezfooli et al, DeepFool: a simple and accurate method to fool deep neural networks, CVPR 2016
        • Use average minimum-distance
        • E_{(x,y) \sim D}[\min_{x' \in A_{x,y}} d(x, x') ]
        • DeepFool approximates this by computing the closest decision boundary
          
          
      • Carlini-Wagner Method (CW)
        • Carlini & Wagner, Towards Evaluating the Robustness of Neural Networks, IEEE S&P 2017
        • CW attempts to directly minimize the distance \| \delta \| in targeted attack
        • \min_{\delta:k(x+\delta)=y_{target}} \| \delta \|_2
        • CW takes the Lagrangian relaxation to allow the gradient-based optimization (Hard constraint -> Soft constraint )
        • \min_{\delta} \| \delta \|_2 + \alpha \cdot g(x + \delta)
   2. Black-box attacks
      • Some Adversarial examples strongly transfer across different networks
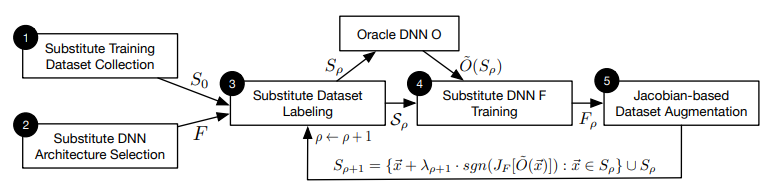
      • The Local Substitute Model
        • Papernot et al, Practical Black-Box Attacks against Machine Learning, ACM CCS 2017
        • Idea : Finding an adversarial example via white-box attack on the local substitute model
        • Goal : Training a local substitute model via FGSM-based adversarial dataset
          
      • Ensemble Based Method
        • Liu et al, Delving into Transferable Adversarial Examples and Black-box Attacks, ICLR 2017
        • Idea : White-box attack to an ensemble of the substitute models
        • Results : The first successful black-box attack against Clarifai.com
   3. Unrestricted and physical attacks
      • Unrestricted
        • So far, all we have considered is about restricted attacks
        • There are much more noise types that humans don’t aware
      • Su et al, One pixel attack for fooling deep neural networks, arXiv 2017
      • Karmon et al, LaVAN : Localized and Visible Adversarial Noise, ICML 2018
      • Engstrom et al, A ROTATION AND A TRANSLATION SUFFICE: FOOLING CNNS WITH SIMPLE TRANSFORMATIONS, arXiv 2017
      • Eykholt et al, Robust Physical-World Attacks on Deep Learning Models, CVPR 2018
      • Xiao et al, Spatially Transformed Adversarial Examples, ICLR 2018
3. Adversarial Defense Methods
   1. Adversarial Training
      • Madry et al, Towards Deep Learning Models Resistant to Adversarial Attacks, ICLR 2018
        • Recall : Adversarial attacks aims to find inputs so that :
           \max_{x':d(x,x')<\epsilon}L(f(x'), y)
        • In the viewpoint of defense, our goal is to minimize the adversarial risk
          E_{(x,y) \sim D}[\max_{x':d(x,x')<\epsilon}L(f(x'), y)]
        • Challenge : Computing the inner-maximization is difficult
        • Idea : Use strong attack methods to approximate the inner-maximization
          • e.g. FGSM, PGD, DeepFool, …
        • Up to now, adversarial training is the only framework that has passed the test-of-time to show its effectiveness against adversarial attack
        • Madry et al. also released the “attack challenges” against their trained models
          • MNIST : https://github.com/MadryLab/mnist_challenge
          • CIFAR10 : https://github.com/MadryLab/cifar10_challenge
   2. Large margin training
      • Elsayed et al, Large Margin Deep Networks for Classification, NeurIPS 2018
        • Minimize the average minimum-distance
          max_{\theta} ( E_{(x,y) \sim D}[\min_{x' \in A_{x,y}} d(x, x') ] ) where A_{x,y} = \{ x': f(x') \not = y\}
        • Large margin training attempts to maximize the margin
   3. Obfuscated gradients : False sense of security
      • Athalye et al, Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples, ICML 2018
        • In ICML 2019, 9 defense papers were published including adversarial training
        • In face, most of them are “fake” defenses
        • They don’t aim the non-existence of adversarial example
        • Rather, they aim to obfuscate the gradient information
        • Obfuscated gradient makes gradient-based attacks (FGSM, PDG, …) harder
        • They identified three obfuscation techniques used in the defenses
          • Shattered Gradients
          • Stochastic Gradients
          • Exploding & Vanishing Gradients
        • Those kinds of defenses can be easily bypassed by 3 simple tricks
          • Backward Pass Differentiable Approximation
          • Expectation Over Transformation
          • Reparametrization
        • Adversarial Training [Madry et al 2018, Na et al 2018] were the only survivals
        • What should we do?
          • At least, we have to do sanity checks
          • Some “red-flags“
   4. Certified Robustness via Wasserstein Adversarial Training
      • Sinha et al, Certifying Some Distributional Robustness with Principled Adversarial Training, ICLR 2018
        • Challenge : attack methods do not fully solve the inner-maximization
          \min_{\theta} (E_{(x,y) \sim D}[\max_{x':d(x,x')<\epsilon}L(f(x'), y)])
        • Motivation : Wasserstein adversarial training considers distributional robustness
        • Wasserstein adversarial training (WRM) outperform the baselines
   5. Tradeoff between accuracy and robustness
      • Zhang et al, Theoretically Principled Trade-off between Robustness and Accuracy, ICML 2018
        •  TRADES ( TRadeoff-inspired Adv. DEfense vis Surrogate-loss minimization)
        • Motivation : Robust leads accuracy reduction ??
        • Re-write the relationship between robust error and natural error
        • Zhang et al (2019) also defines the boundary error
        • Up to now, TRADES is regarded as the state-of-the-art defense method
4. Future Research Area
   1. Increase robustness maintaining clean accuracy
   2. applications : salience map, image-to-image translation