2020 인공지능학회 동계강좌를 신청하여 2020.1.8 ~ 1.10 3일 동안 다녀왔다. 총 9분의 연사가 나오셨는데, 프로그램 일정은 다음과 같다.
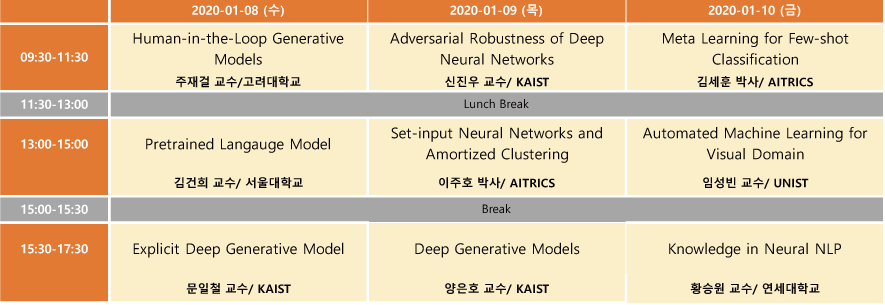
전체를 묶어서 하나의 포스트로 작성하려고 했는데, 주제마다 내용이 꽤 많을거 같아, 한 강좌씩 시리즈로 묶어서 작성하게 되었다. 네 번째 포스트에서는 KAIST 신진우 교수님의 “Adversarial Robustness of Deep Neural Networks” 강연 내용을 다룬다.
- Introduction
- What is The Adversarial Example?
- Problem : ML Systems are highly vulnerable to a small noise on input that are specifically designed by an adversary.
- Threat of Adversarial Examples
- Adversarial examples raise issues critical to the “AI safety” in the real world.
- Adversarial examples exist across various tasks or modalities, ex) segmentation, speech recognition
- The Adversarial Game : Attacks and Defenses
- Attacks : Design inputs for a ML system to produce erroneous outputs
- Defenses : Prevent the misclassification by adversarial examples
- Threat Model
- Adversary goals : simply to cause misclassification or attack into a target class
- Adversary capabilities : reasonable constraints to adversary
- To date, most defenses restrict the adversary to make “small” changes to inputs d(x, x') < \epsilon
- a common choice for d(\cdot, \cdot) is l_p distance
- Adversary knowledge
- White-box model : Complete knowledge
- Black-box model : No knowledge of the model
- Gray-box : A limited number of queries to the model
- Evaluating Adversarial Robustness
- “Adversarial Risk” : The worst-case loss L for a given perturbation budget
- E_{(x,y) \sim D}[\max_{x':d(x,x')<\epsilon}L(f(x'), y)]
- Objective : Minimize
- Cons : one must decide \epsilon
- SOTA : FSGM, PGD (explained in later)
- The average minimum-distance of the adversarial perturbation
- E_{(x,y) \sim D}[\min_{x' \in A_{x,y}} d(x, x') ]
- Objective : Maximize (Maximize minimum margin)
- SOTA : CW (Carlini & Wagner, explained in later )
- “Adversarial Risk” : The worst-case loss L for a given perturbation budget
- What is The Adversarial Example?
- Adversarial Attack Methods
- White-box attacks
- Fast Gradient Sign Method (FGSM)
- Goodfellow et al, Explaining and Harnessing Adversarial Examples, ICLR 2015
- Goal : Untargeted Attack, Find argmax_{x':d(x,x')<\epsilon}L(f(x'),y)
- Capabilities : Pixel-wise restriction : d(x,x')=\| x-x' \|_{\infty} := \max_i |x_i - x'_i | \leq \epsilon
- Knowledge : White-box
- Least-likely Class Method
- Kurakin et al, Adversarial Machine Learning at Scale, ICLR 2017
- Goal : Targeted Attack
- Capabilities : Pixel-wise restriction : d(x,x')=\| x-x' \|_{\infty} := \max_i |x_i - x'_i | \leq \epsilon
- Knowledge : White-box
- Projected Gradient Descent (PGD)
- Madry et al, Towards Deep Learning Models Resistant to Adversarial Attacks, ICLR 2018
- \max_{x' \in x + B} L(f(x'), y) , where B is the set of neighbors
- In some sense, PGD is regarded as the strongest first-order adversary
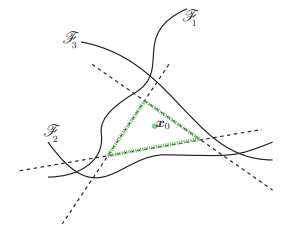
- DeepFool
- Moosavi-Dezfooli et al, DeepFool: a simple and accurate method to fool deep neural networks, CVPR 2016
- Use average minimum-distance
- E_{(x,y) \sim D}[\min_{x' \in A_{x,y}} d(x, x') ]
- DeepFool approximates this by computing the closest decision boundary
- Carlini-Wagner Method (CW)
- Carlini & Wagner, Towards Evaluating the Robustness of Neural Networks, IEEE S&P 2017
- CW attempts to directly minimize the distance \| \delta \| in targeted attack
- \min_{\delta:k(x+\delta)=y_{target}} \| \delta \|_2
- CW takes the Lagrangian relaxation to allow the gradient-based optimization (Hard constraint -> Soft constraint )
- \min_{\delta} \| \delta \|_2 + \alpha \cdot g(x + \delta)
- Fast Gradient Sign Method (FGSM)
- Black-box attacks
- Some Adversarial examples strongly transfer across different networks
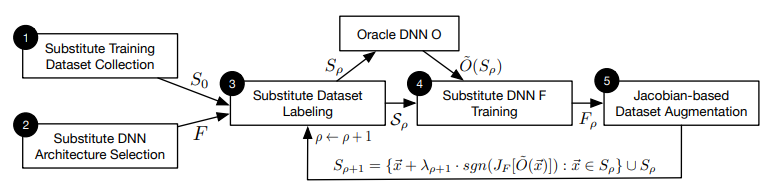
- The Local Substitute Model
- Papernot et al, Practical Black-Box Attacks against Machine Learning, ACM CCS 2017
- Idea : Finding an adversarial example via white-box attack on the local substitute model
- Goal : Training a local substitute model via FGSM-based adversarial dataset
- Ensemble Based Method
- Liu et al, Delving into Transferable Adversarial Examples and Black-box Attacks, ICLR 2017
- Idea : White-box attack to an ensemble of the substitute models
- Results : The first successful black-box attack against Clarifai.com
- Unrestricted and physical attacks
- Unrestricted
- So far, all we have considered is about restricted attacks
- There are much more noise types that humans don’t aware
- Su et al, One pixel attack for fooling deep neural networks, arXiv 2017
- Karmon et al, LaVAN : Localized and Visible Adversarial Noise, ICML 2018
- Engstrom et al, A ROTATION AND A TRANSLATION SUFFICE: FOOLING CNNS WITH SIMPLE TRANSFORMATIONS, arXiv 2017
- Eykholt et al, Robust Physical-World Attacks on Deep Learning Models, CVPR 2018
- Xiao et al, Spatially Transformed Adversarial Examples, ICLR 2018
- Unrestricted
- White-box attacks
- Adversarial Defense Methods
- Adversarial Training
- Madry et al, Towards Deep Learning Models Resistant to Adversarial Attacks, ICLR 2018
- Recall : Adversarial attacks aims to find inputs so that :
\max_{x':d(x,x')<\epsilon}L(f(x'), y) - In the viewpoint of defense, our goal is to minimize the adversarial risk
E_{(x,y) \sim D}[\max_{x':d(x,x')<\epsilon}L(f(x'), y)] - Challenge : Computing the inner-maximization is difficult
- Idea : Use strong attack methods to approximate the inner-maximization
- e.g. FGSM, PGD, DeepFool, …
- Up to now, adversarial training is the only framework that has passed the test-of-time to show its effectiveness against adversarial attack
- Madry et al. also released the “attack challenges” against their trained models
- Recall : Adversarial attacks aims to find inputs so that :
- Madry et al, Towards Deep Learning Models Resistant to Adversarial Attacks, ICLR 2018
- Large margin training
- Elsayed et al, Large Margin Deep Networks for Classification, NeurIPS 2018
- Minimize the average minimum-distance
max_{\theta} ( E_{(x,y) \sim D}[\min_{x' \in A_{x,y}} d(x, x') ] ) where A_{x,y} = \{ x': f(x') \not = y\} - Large margin training attempts to maximize the margin
- Minimize the average minimum-distance
- Elsayed et al, Large Margin Deep Networks for Classification, NeurIPS 2018
- Obfuscated gradients : False sense of security
- Athalye et al, Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples, ICML 2018
- In ICML 2019, 9 defense papers were published including adversarial training
- In face, most of them are “fake” defenses
- They don’t aim the non-existence of adversarial example
- Rather, they aim to obfuscate the gradient information
- Obfuscated gradient makes gradient-based attacks (FGSM, PDG, …) harder
- They identified three obfuscation techniques used in the defenses
- Shattered Gradients
- Stochastic Gradients
- Exploding & Vanishing Gradients
- Those kinds of defenses can be easily bypassed by 3 simple tricks
- Backward Pass Differentiable Approximation
- Expectation Over Transformation
- Reparametrization
- Adversarial Training [Madry et al 2018, Na et al 2018] were the only survivals
- What should we do?
- At least, we have to do sanity checks
- Some “red-flags“
- Athalye et al, Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples, ICML 2018
- Certified Robustness via Wasserstein Adversarial Training
- Sinha et al, Certifying Some Distributional Robustness with Principled Adversarial Training, ICLR 2018
- Challenge : attack methods do not fully solve the inner-maximization
\min_{\theta} (E_{(x,y) \sim D}[\max_{x':d(x,x')<\epsilon}L(f(x'), y)]) - Motivation : Wasserstein adversarial training considers distributional robustness
- Wasserstein adversarial training (WRM) outperform the baselines
- Challenge : attack methods do not fully solve the inner-maximization
- Sinha et al, Certifying Some Distributional Robustness with Principled Adversarial Training, ICLR 2018
- Tradeoff between accuracy and robustness
- Zhang et al, Theoretically Principled Trade-off between Robustness and Accuracy, ICML 2018
- TRADES ( TRadeoff-inspired Adv. DEfense vis Surrogate-loss minimization)
- Motivation : Robust leads accuracy reduction ??
- Re-write the relationship between robust error and natural error
- Zhang et al (2019) also defines the boundary error
- Up to now, TRADES is regarded as the state-of-the-art defense method
- Zhang et al, Theoretically Principled Trade-off between Robustness and Accuracy, ICML 2018
- Adversarial Training
- Future Research Area
- Increase robustness maintaining clean accuracy
- applications : salience map, image-to-image translation