가설검정 (Hypothesis Testing) – Type Ⅱ Error 확률 계산과 Z-Test Sample Size 찾기

This entry is part 3 of 8 in the series 가설검정

가설검정

 

 

 

 

 

이번 포스트는 가설검정의 세 번째 포스트로 Type Ⅱ Error 확률 계산과 Z-Test Sample Size 찾기 (Calculating Type Ⅱ Error Probabilities and Finding the Sample Size for the Z Test) 를 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.

3. Type Ⅱ Error 확률 계산과 Z-Test Sample Size 찾기 (Calculating Type Ⅱ Error Probabilities and Finding the Sample Size for the Z Test)

Type Ⅱ Error 는 ‘2종 과오 확률’ 로 번역되며, \beta 로 표기한다. 일반적으로 통계 검정에서  \beta 를 계산하는 것은 쉽지 않지만, 앞 선 포스트에서 살펴본 Z test 와 같은 다(多) 표본 검정에서는 비교적 간단하다. 이 장에서는  \beta 확률을 도출하고, 검정에 적합한 Sample Size 를 찾는 두 가지 작업에 대해 알아볼 것이다.

다음과 같은 귀무가설 H0 와 대립가설 Ha 에 대해서, Type Ⅱ Error 는 Ha 를 만족하는 \theta 에 대해서 계산할 수 있다.

H0 : \theta = \theta_0

Ha : \theta > \theta_0

실험자가 대립가설이 옳다고 생각한다면, 즉 \theta = \theta_a (where \theta_a > \theta_0 ), 기각역은

RR= \{\hat{\theta}:\hat{\theta}>k\}

 

이므로, type Ⅱ Error,  \beta 는

\beta = P( Ha 가 참일 때,  \hat{\theta} 가 기각역에 있지 않은 경우) = 대립가설이 참일 때, 귀무가설이 기각되지 않을 확률

 

이며,

\beta = P(\hat{\theta} \leq k~when~\theta = \theta_a)~=~P(\dfrac{\hat{\theta}-\theta_a}{\sigma_{\hat{\theta}}} \leq \dfrac{k-\theta_a}{\sigma_{\hat{\theta}}}~when~\theta=\theta_a)

 

와 같이 전개할 수 있다. 여기서 \theta_a 가 \theta 에 대한 참 값일 때, \dfrac{\hat{\theta}-\theta_a}{\sigma_{\hat{\theta}}} 는 근사적으로 표준 정규 분포를 따른다. 따라서  \beta 의 확률은 표준 정규 분포 곡선에서 찾을 수 있다.

고정된 Sample Size, n 에 대해서  \beta 의 크기는 \theta_a 와  \theta_0 의 거리에 따라 정해진다. \theta_a 가 \theta_0 와 가까우면, \theta 에 대한 참 값 ( \theta_a 혹은 \theta_0 ) 는 찾기 어려워지고, Ha 가 참일 때 귀무가설 H0 를 채택할 확률은 커진다.  \theta_a 가 \theta_0 와 멀리 떨어져 있으면, 참 값은 상대적으로 찾기 쉽고  \beta 도 상당히 작아진다. 앞 포스트에서 살펴 보았듯이 Sample Size, n 을 크게 잡으면 \alpha, \beta 는 함께 작게 될 수 있다.

예제1.앞 포스트 예제1. 에서 나온 부사장이 평균 영업사원들의 일주일당 고객 전화 횟수에 1만큼 차이가 있음을 확인하고 싶다고 한다. 즉, 그는 H_0:~\mu=15 against H_a:~\mu=16 를 검정하고 싶다. 앞의 예제의 데이터를 갖고  type Ⅱ Error,  \beta 를 찾아라.

풀이.

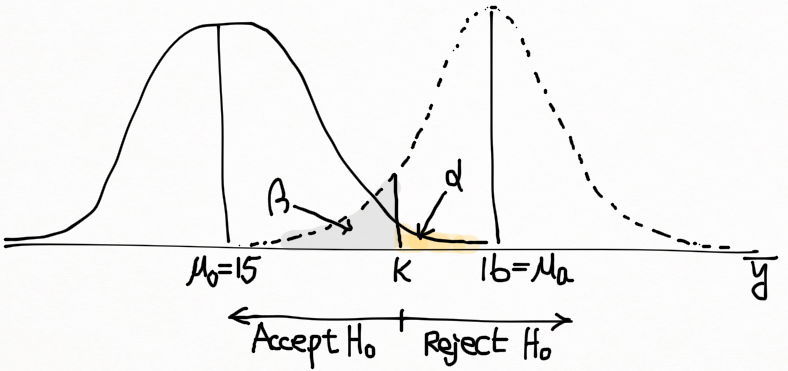
앞선 풀이에서 n=36,~\bar{y}=17 그리고 s^2=9 였다. 0.05 레벨에 대한 기각역은,

z=\dfrac{\bar{y}-\mu_0}{\sigma/\sqrt{n}}>1.645

였다. 이것은 다음과 같으므로,

\bar{y}-\mu_0>1.645(\dfrac{\sigma}{\sqrt{n}})~or~\bar{y}>\mu_0+1.645(\dfrac{\sigma}{\sqrt{n}})

 

\mu_0=15 그리고, n=36 을 대입하고 \sigma 는 s 로 근사하면 기각역은 다음과 같이 계산 할 수 있다.

\bar{y}>15+1.645(\dfrac{3}{36}) 혹은 동일하게, \bar{y}>15.8225

 

이 기각역이 위의 그림에 표시되어 있다. 정의에 의해서 \beta = P(\bar{Y} \leq 15.8225~when~\mu=16) 이 점선으로 나타나는 곡선 아래의 k=15.8225 왼편의 음영 영역이다. 따라서, \mu_a=16 에 대해서

\beta = P(\dfrac{\bar{Y}-\mu_a}{\sigma/\sqrt{n}} \leq \dfrac{15.8225-16}{3/\sqrt{36}})=P(Z \leq -0.36)=0.3594

 

이런 큰  \beta 값은, “sample size, n = 36인 경우, 가설로 세운 평균이 1 만큼 차이날 때 종종 실패한다는 것을 보여준다.” sample size, n 을 늘리므로써 \beta 값을 줄일 수 있다.

 

앞선 예제는 실험자가 실험을 위한 sample size 를 선택할 때, 사용할 수 있는 절차를 제안합니다.

우리가 귀무가설 H0 : \mu = \mu_0 과 대립가설 Ha: \mu>\mu_0 를 검증하려고 한다고 가정해 보자. 만약 특정 \alpha 와 \beta 값을 원한다고 하면 ( \beta 는 \mu = \mu_a 그리고 \mu_a > \mu_0 일 때 계산된다. ), 다음 두 가지 양은 실험으로 추가적으로 조정할 수 있다: sample size, n 과 기각역이 시작되는 위치, k.  \alpha 와 \beta 는 n 과 k 를 포함한 식으로 표현할 수 있으며 이 2개의 식은 2개의 미지수를 갖고 있으므로 n 에 대해서 동시에 소거할 수 있다. 즉,

\alpha = P(\bar{Y}>k~when~\mu=\mu_0) =P(\dfrac{\bar{Y}-\mu_0}{\sigma/\sqrt{n}}>\dfrac{k-\mu_0}{\sigma/\sqrt{n}}~when~\mu=\mu_0)=P(Z>z_{\alpha})

 

\beta = P(\bar{Y} \leq k~when~\mu=\mu_a) P(\dfrac{\bar{Y}-\mu_a}{\sigma/\sqrt{n}} \leq \dfrac{k-\mu_a}{\sigma/\sqrt{n}}~when~\mu=\mu_a)=P(Z \leq -z_{\beta})

 

위 두 식에서 알아본  \alpha 와 \beta 는

\dfrac{k-\mu_0}{\sigma/\sqrt{n}}=z_{\alpha} and \dfrac{k-\mu_a}{\sigma/\sqrt{n}}=-z_{\beta}

이 된다. 여기서 k 를 소거하면

\mu_0+z_{\alpha}(\dfrac{\sigma}{\sqrt{n}})=\mu_a-z_{\beta}(\dfrac{\sigma}{\sqrt{n}})

 

이고,

(z_{\alpha}+z_{\beta})(\dfrac{\sigma}{\sqrt{n}})=\mu_a-\mu_0

 

혹은 동일하게

\sqrt{n} = \dfrac{(z_{\alpha}+z_{\beta})\sigma}{(\mu_a-\mu_0)} 가 된다.

Upper-Tail α-Level Test 의 Sample Size

n = \dfrac{(z_{\alpha}+z_{\beta})^2\sigma^2}{(\mu_a-\mu_0)^2}

 

예제1.앞 포스트 예제1. 에서 H_0:~\mu=15 against H_a:~\mu=16,  \alpha=\beta=0.05 를 만족하는 sample size 를 찾아라. ( \sigma^2 는 근사적으로 9 라고 가정한다. )

풀이.

\alpha=\beta=0.05 이므로, z_{\alpha}=z_{\beta}=z_{0.05}=1.645 이다. 따라서,

 

n = \dfrac{(z_{\alpha}+z_{\beta})^2\sigma^2}{(\mu_a-\mu_0)^2}=\dfrac{(1.645+1.645)^2(9)}{(16-15)^2}=97.4

 

따라서, n =98 일 때 \alpha\approx\beta\approx 0.05 를 만족한다고 할 수 있다.

Series Navigation<< 가설검정 (Hypothesis Testing) – 다(多) 표본 검정가설검정 (Hypothesis Testing) – 가설검정절차와 신뢰구간사이의 관계 >>

2 thoughts on “가설검정 (Hypothesis Testing) – Type Ⅱ Error 확률 계산과 Z-Test Sample Size 찾기”

  1. 안녕하세요, 글 잘 읽었습니다.
    궁금한 점이 한가지 있는데요, 예제1에서 베타값에 대한 기각역을 구할 때 upper tailed 로 구하셨는데, 위 대립가설의 경우에는 u = 16 이라고 되어있어서 어떤식으로 upper level로 판단하셨는지 알고 싶습니다. 제가 막 공부하는 입장이라 대립가설의 형태가 위와 같은 경우도 처음봐서 기각역을 구하는 부분이 잘 이해가 안되네요 ㅎㅎ;

    응답

    • 안녕하세요? 본문을 보시면, ‘θ hat’ 이 θ 보다 크다는 가정을 하고 θa 를 16으로 잡고 있습니다. 따라서 가정에 의해 Upper Tail Test 를 수행한 것으로 보시면 됩니다. 그리고 16이란 숫자는 예제를 풀기위해 설정된 숫자입니다. 예제1.의 내용에 부사장이 1만큼의 차이가 있다는 것을 확인한다는 말을 Lower Tail 방향이라고 생각하실 수도 있지만 앞 포스트에서 기각역을 설정할 때 이미 Upper Tail Test 를 가정하고 있으므로 연속된 문제에서도 Upper Tail Test 동일하게 설정하고 있습니다. 또 그렇게 해야 아래의 Sample Size 를 구하는 부분까지 연결이 되기 때문입니다.

      응답

Leave a Comment