가설검정 (Hypothesis Testing) – 소(小) 표본 가설검정; μ 그리고 μ1 – μ2

 

 

 

 

 

이번 포스트는 가설검정의 일곱 번째 포스트로 소(小) 표본 가설검정; μ 그리고 μ1 – μ2 (Small-Sample Hypothesis Testing for μ and μ1 – μ2) 를 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.

7. 소(小) 표본 가설검정; μ 그리고 μ1 – μ2 (Small-Sample Hypothesis Testing for μ and μ1 – μ2 )

앞선 포스트에서 다(多) 표본 가설 검정 절차에 대해 알아보았었다. 다 표본 문제에서 구간 추정(interval estimation) 절차는 유용하게 사용되었다. 이런 방법들은 표본 수가 충분히 클 경우여야 하는데, 즉 Z = (\hat{\theta} - \theta_0)/\sigma_{\hat{\theta}} 가 표준 정규분포에 근사될 수 있음을 말한다. 추정-6번째 포스트에서  μ나 (단일 정규 모집단 평균)  μ1 – μ2 (등분산인 두 개의 정규 모집단의 평균의 차이) 의 신뢰구간을  t 분포에 기초하여 형성할 수 있다. 이 장에서는 정규 모집단으로부터의 소 표본에 적합한 μ 와 μ1 – μ2 에 대한 가설 검정 방법을 형성해 보겠다.

Y_1, Y_2, ... , Y_n 를 모 평균 μ 와 모 분산 σ² 을 모르는 크기 n 인 랜덤 샘플이라고 지칭하자. \bar{Y} 와 S 를 표본평균과 표본표준편차라고 할 때, 귀무가설 H₀ : μ = μ₀ 가 참일 때,

T = \dfrac{\bar{Y} - \mu_0}{S/\sqrt{n}}

는 n-1 의 자유도를 갖는 t 분포를 따른다.

t 분포가 대칭적으로 가운데가 불룩한 형상이므로, 귀무가설 H₀ : μ = μ₀ 에 대한 소 표본 검정의 기각역은 t 분포의 꼬리쪽에 위치하며, 다 표본 Z 통계량과 마찬가지 방식으로 결정할 수 있다. Z 검정과 유사하게 upper-tail 대립가설 Ha : μ > μ₀ 에 대한 올바른 기각역은 다음과 같다.

RR = \{ t > t_{\alpha} \}

 

여기서 t_{\alpha} 는 n-1 자유도의 t 분포에 대해 P\{T > t_{\alpha}\} = \alpha 를 만족하는 값이다.

t 분포를 기초한  μ 에 대한 검정 (t-test 라고 알려진)을 정리하면 아래와 같다.

μ 에 대한 소 표본 검정 가정 : Y_1, Y_2, ... , Y_n 은 E(Y_i) =\mu 인 정규 분포로부터 얻어진 랜덤 표본이라고 하자. H_0~:~\mu =\mu_0   H_a=\begin{cases} \mu > \mu_0~~~~(upper~tail~alternative) \\ \mu < \mu_0~~~~(lower~tail~alternative) \\ \mu \not= \mu_0~~~~(two~tailed~alternative) \end{cases}   검정 통계량 :  T = \dfrac{\bar{Y} - \mu_0}{S/\sqrt{n}}   기각역 :  \begin{cases} t > t_{\alpha}~~~~~~~~~(upper~tail~RR) \\t <-t_{\alpha}~~~~~~(lower~tail~RR) \\|t| > t_{\alpha/2}~~~~(two~tailed~RR) \end{cases}

 

예제 1. 새로운 화약에 대한 8개 탄환에 대한 총구의 속도에 대해 표본 평균과 표본 표준편차가 \bar{y} = 2959 , s = 39.1 로 관측되었다. 제조사는 새로운 화약으로 총구의 속도가 적어도 3000 ft/sec 이상일 것이라고 주장한다. 표본 관측결과가 이 주장을 뒷받침할 만한 충분한 근거가 되는지 0.025 유의수준으로 검증하라.

풀이.

총구 속도가 근사적으로 정규 분포를 띈다고 가정하자. 귀무가설 H₀ : μ = 3000 에 대해 대립가설 Ha : μ < 3000 을 검증하면 된다. t 분포가 자유도 v = n – 1 = 7 을 갖고 있으므로 기각역은 t < -t_{0.025} =-2.365 로 주어진다. 계산하면 검정 통계량을 얻을 수 있다.

t = \dfrac{\bar{y}-\mu_0}{s/\sqrt{n}} = \dfrac{2959-3000}{39.1/\sqrt{8}}=-2.966

 

이 값은 기각역에 속하므로 (즉, t = -2.966 이 -2.365 보다 작기 때문에), 귀무가설은 유의수준 α = 0.025 에서 기각된다. 따라서 제조사의 주장에 대치되는 충분한 증거를 발견했다고 주장할 수 있다.

 

예제 2. 예제 1에서의 p-value 는 무엇인가?

풀이.

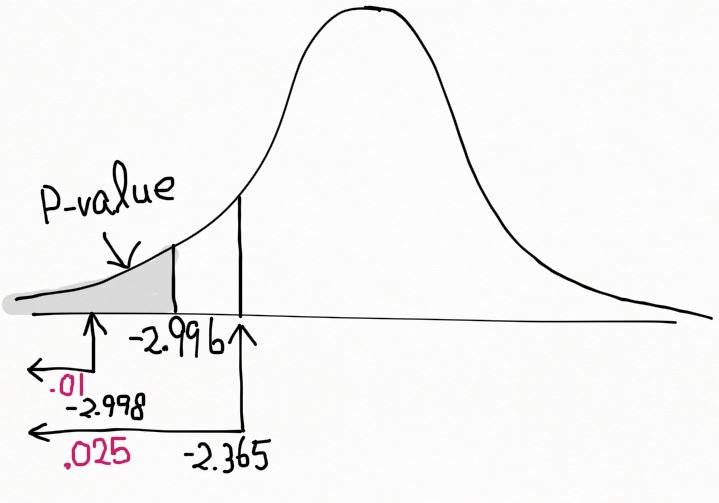
만약 t가 작으면 귀무가설이 기각되므로, 귀무가설이 기각될 수 있는 가장 작은 α 값이 p-value 가 된다. (T < -2.966); T가 n-1 = 7 의 자유도를 갖는 t 분포를 따를 때.

-2.966은 t 분포표 상에서 d.f. = 7 인 행의 -t_0.025 = -2.365 와 -t_0.01 = -2.998 사이에 위치하므로, 0.01 ≤ p-value ≤ 0.025 이다.

(실제 R 이나 통계 Tool 을 돌리면 p-값을 바로 계산할 수 있다.)

 

t 분포에 대한 두 번째 응용은 두 개의 정규 모집단이 동일한 분산 (등분산)을 가질 때 소 표본으로부터 모 집단의 평균을 비교하는 것이다. Y_{11}, Y_{12}, ... , Y_{1n_1} 을 첫 번째,  Y_{21}, Y_{22}, ... , Y_{2n_2} 를 두번 째 표본이라고 할 때 i 번째 모집단의 평균과 분산은 \mu_i, \sigma^2, ~for~ i = 1, 2 가 된다. \bar{Y_i} 와 S^2_i, ~for ~i = 1, 2 를 표본 평균과 표본 분산이라고 가정하자. 가정을 만족할 때 추정-8번째 포스트에서 도출한 pooled estimator for \sigma^2 는

S^2_p = \dfrac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2}

 

이며, 통계량 T 는

T = \dfrac{(\bar{Y_1}-\bar{Y_2})-(\mu_1-\mu_2)}{S_p\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}

 

는 n_1+n_2-2 의 자유도를 갖는 Student’s t 분포를 갖는다. 만약 우리가 귀무가설 H₀: μ₁-μ₂ = D₀ (고정된 값 D₀) 을 검정하고 싶다면 H0 가 참일 때

T = \dfrac{\bar{Y_1}-\bar{Y_2}-D_0}{S_p\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}

 

는 n_1+n_2-2 의 자유도를 갖는 Student’s t 분포를 갖는다. 소 표본 검정의 통계량은 다 표본 검정 Z 통계량과 유사하다는 것을 인지하기 바란다. 귀무가설 H₀: μ₁-μ₂ = D₀ 에 대한 upper-tail, lower-tail, two-tailed alternatives 들은 다 표본 검정에서와 같은 방식으로 성립할 수 있다. μ₁-μ₂ 에 대한 소 표본 검정 절차는 아래와 같이 정리할 수 있다.

두 모집단 평균 비교에 대한 소 표본 검정 H_0~:~\mu_1-\mu_2=D_0   H_a~:~\begin{cases} \mu_1-\mu_2>D_0~~~~~(upper~tail~alternative) \\ \mu_1-\mu_2<D_0~~~~~(lower~tail~alternative) \\ \mu_1-\mu_2 \not=D_0~~~~~(two-tailed~alternative) \end{cases}   검정 통계량 : T = \dfrac{\bar{Y_1}-\bar{Y_2}-D_0}{S_p\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}   ,where~S^2_p = \dfrac{(n_1-1)S^2_1+(n_2-1)S^2_2}{n_1+n_2-2}   기각역 :  \begin{cases} t > t_{\alpha}~~~~~~~~~(upper~tail~RR) \\t <-t_{\alpha}~~~~~~(lower~tail~RR) \\|t| > t_{\alpha/2}~~~~(two~tailed~RR) \end{cases}   P(T>t_{\alpha})=\alpha 이고, 자유도 \nu = n_1+n_2-2

 

예제 3. 다른 훈련을 받은 제조 작업자들 사이에 단일 조립공정의 완료 시간을 측정한 데이터를 얻었다. 표본 데이터는 아래 표와 같다. 표준 방식 새로운 방식 n_1 = 9 \bar{y_1}=35.22 seconds   \sum^9_{i=1}(y_{1i}-\bar{y_1})^2 =195.56 n_2 = 9 \bar{y_2}=31.56 seconds   \sum^9_{i=1}(y_{2i}-\bar{y_2})^2 =160.22 이 두 훈련 방법에 따른 조립 시간에 차이가 있다고 말할 충분한 근거가 있는지 α = 0.05 유의수준에서 검증하라.

풀이.

귀무가설 H_0~:~(\mu_1-\mu_2)=0 에 대한 대립가설  H_a~:~(\mu_1-\mu_2)\not=0 을 검정해야 하고, 양측 검정(two-tailed test)에 속한다. 검정 통계량은

T = \dfrac{(\bar{Y_1}-\bar{Y_2})-D_0}{S_p\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}

 

D_0 = 0 이며 유의수준 \alpha=0.05 에 대한 기각역은 |t|>t_{\alpha/2}=t_{0.025} 이다. 자유도 \nu =(n_1+n_2-2) = 9+9-2 = 16 이므로 t_{0.025}=2.120 이다.

관측된 값으로부터 검정 통계량을 계산하면,

s_p = \sqrt{s^2_p}=\sqrt{\dfrac{195.56+160.22}{9+9-2}}=\sqrt{22.24}=4.716

 

이고,

t=\dfrac{\bar{y_1}-\bar{y_2}}{s_p\sqrt{\dfrac{1}{n_1}+\dfrac{1}{n_2}}}=\dfrac{35.22-31.56}{4.716\sqrt{\dfrac{1}{9}+\dfrac{1}{9}}}=1.65

 

이 값은 기각역 ( |t|>2.120) 에 속하지 않으므로, 귀무가설을 기각할 수 없다. 따라서 두 훈련 방식에 따른 작업자들 사이의 조립시간에 차이가 있다는 주장에는 충분한 근거가 부족하다.

다만, 앞의 포스트에서 언급했듯이 우리는 아직 귀무가설  H_0~:~(\mu_1-\mu_2)=0 를 채택하진 않았다. 대신에 대립가설  H_a~:~(\mu_1-\mu_2)\not=0  을 채택하고 귀무가설 H₀ 를 기각할 충분한 근거를 얻지 못했다고 기술할 수 있다.

 

예제 4. 예제 3에서의 p-value 는 무엇인가?

풀이.

관측된 값으로부터 얻은 t 값은 t = 1.65 였다. p-value 는 아래 그림의 음영 영역처럼, T > 1.65 와 T < -1.65 인 두 확률을 더한 값이다. 즉 A1 + A2.

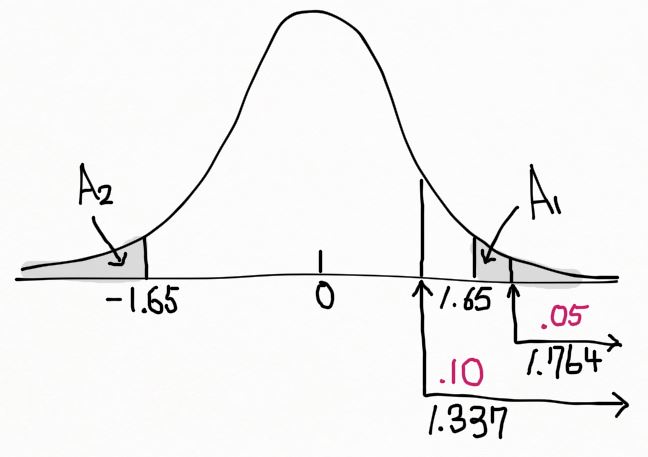
t 통계량이 자유도 n_1+n_2-2 = 16 에 기초하므로 t 분포표에서 t_{0.05} = 1.746 이고  t_{0.1} = 1.337 이므로, A_1 = P(T>1.65) 는 0.05와 0.1 사이에 위치한다. 즉, 0.05 < A1 < 0.1 마찬가지로 0.05 < A2 < 0.1 이다. p-value 는 A1 + A2 이므로 0.1 < p-value < 0.2 가 된다. 이 예제의 경우 유의수준 α = 0.05 이므로 귀무가설을 기각할 수 없었다.

 

 

예제1. 에서 총구의 속도는 정규 모집단에서 랜덤 표본으로 부터 관측되었다고 가정하였다. 대부분의 경우에 이 가정을 증명하기가 어렵다. 이 곤궁한 상황이 결론의 유효성에 어떤 영향을 미치는지 물어볼 필요가 있다.

\dfrac{\bar{Y}-\mu}{S/\sqrt{n}}

 

위 통계량에 대해 비정규 모집단에 대한 표본추출등의 경험적인 연구들이 시도되었다. 이런 조사를 통해서 모집단이 정규성에 살짝 벗어나는 것은 (moderate departures from normality) 검정 통계량에 아주 작은 영향을 미친다는 것이 증명되었다. 이 결과를 통해 근사적으로 정규성을 갖는 데이터들로부터 모집단의 평균에 대한 검정을 t 검정을 통해서 아주 효과적으로 수행할 수 있다. 통계 검정이 가정에 민감하지 않다는 것은 활용성이 높다는 것을 뜻한다. 가정에 대한 비 민감도(insensitivity) 때문에 그것들은 강건한 통계 검정 (robust statistical test) 라고 불린다.

단일 평균에 대한 t-test 와 같이, 두 모집단 평균의 비교의 t-test (종종 two-sample t test 라고 불린다) 역시 정규성 가정에 강건하다. 또 그것은 n_1 이 n_2 와 같거나 (거의 같을 때) \sigma^2_1 =\sigma^2_2 이어야 한다는 가정에도 강건하다.

Series Navigation

<< 가설검정 (Hypothesis Testing) – 가설 검정의 이론에 대한 추가 설명가설검정 (Hypothesis Testing) – 분산에 관련된 가설검정 >>