추정 (Estimation) – 점 추정량의 적합성 산출

 

 

 

 

 

이번 포스트는 추정(Estimation) 의 네 번째 포스트로 점 추정량의 적합성 산출 (Evaluating the Goodness of a Point Estimator) 를 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.

 

4. 점 추정량의 적합성 산출 (Evaluating the Goodness of a Point Estimator)

 

한 가지 방법은 점 추정량과 타겟 파라미터의 거리를 측정하는 것이다. 이를 ‘추정 오차’ (error of estimation) 라 부른다.

정의. 추정 오차 (error of estimation) 은 추정량과 타겟 파라미터 사이의 거리이다. \epsilon=|\hat{\theta}-\theta|

\hat{\theta} 이 랜덤 변수이므로, 추정 오차 또한 랜덤 수량이며 얼마의 값을 갖는지 알수 없다. 하지만 확률로 계산할 수 있다. 예를 들어  \hat{\theta} 가  \theta 의 불편추정량이라고 할 때, 표본 분포를 아래 그림과 같이 갖는다고 하자.

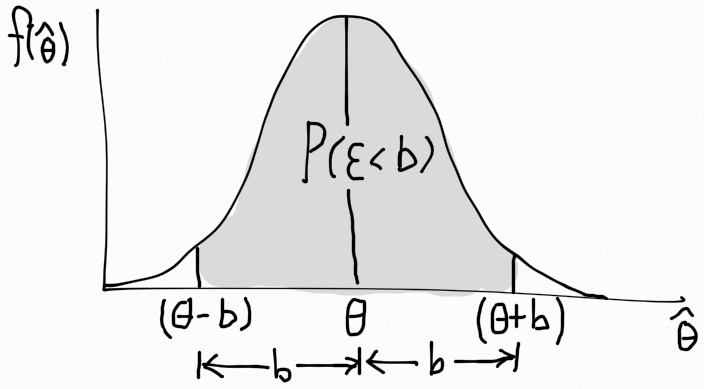
만약 우리가 분포의 양 꼬리쪽에 위치한 두 개의 점 (\theta-b) 와  (\theta+b) 를 선택한다면, 추정 오차 \epsilon 이 b 보다 작을 확률은 그림의 색칠한 부분이 된다. 즉,

P(|\hat{\theta}-\theta| < b)=P[-b< (\hat{\theta}-\theta) < b]=P(\theta-b<\hat{\theta}<\theta+b)

 

우리는 b 를 추정 오차의 확률적인 경계값으로 생각할 수 있다. 비록 오차가 b 보다 작다라고 확실 할 순 없지만, 확률 P(\epsilon<b) 가 크다는 것은 안다.

만일  \hat{\theta} 의 확률 분포를 안다면 확률을 적분하여 특정 확률을 만족하는 b 값을 구할 수 있을 것이다. 예를 들어  P(\epsilon<b) = 0.9 인 b 를 구하고 싶으면,

\int_{\theta-b}^{\theta+b} {f(\hat{\theta})}\,{d}{\hat{\theta}}=0.9

 

 

 

를 풀어내면 된다. 하지만 \hat{\theta} 의 분포를 모르더라도  \hat{\theta} 이 unbiased estimator 라면 b 값을 \hat{\theta} 의 표준 오차의 배수로 근사할 수 있다. 예를들어 b = k\sigma_{\hat{\theta}} 처럼 말이다. Tchebysheff’s theorem 을 통해 \epsilon 이 k\sigma_{\hat{\theta}} 일 확률이 적어도 1- 1/k^2 가 되는 걸 알 수 있다. 가장 편하게는 k=2 를 선택하는 것인데 b= 2\sigma_{\hat{\theta}} 가 되고 적어도 0.75의 확률을 갖는다.

대부분의 랜던 변수들은 2σ 안에 놓일 확률이 95% 근방이다. 아래 표에서 몇 가지 확률 분포의 2σ 안에 놓일 확률을 표시했다.

Distribution	Probability
Normal	0.9544
Uniform	1.0000
Exponential	0.9502

Probability that (μ-2σ) <Y< (μ+2σ)

 

예제. 표본 수 n = 1000 명의 유권자 (랜덤하게 선택된) 중에서 John 을 지지하는 수 y = 560 이었다. John 의 지지율 p (모 파라미터) 를 추정하고 2σ 구간의 b 값을 구하라.

추정량으로 \hat{p} = Y /n 을 사용한다.

\hat{p}=\dfrac{y}{n}=\dfrac{560}{1000}=0.56

 

n 이 아주 크므로  \hat{p} 는 정규분포를 근사한다고 할 수 있고, b= 2\sigma_{\hat{p}} 이면 \epsilon 이 b보다 작을 확률이 대략 0.95 가 된다. 포스트 앞의 표준 오차 값은 \sigma_{\hat{p}} = \sqrt{pq/n} 이기 때문에,

b = 2\sigma_{\hat{p}}=2\sqrt{\dfrac{pq}{n}}

 

여기서 모 파라미터 p 를 정확히 알기 어렵기 때문에 근사적으로 \hat{p} 로 대치한다.

b =2\sigma_{\hat{p}}=2\sqrt{\dfrac{pq}{n}}\approx 2\sqrt{\dfrac{(0.56)(0.44)}{1000}}=0.03

 

우리 계산의 추정 오차는 95%의 확률로 0.03 보다 작다. 우리가 추정한 0.56 의 지지율 추정량은 실제 p 값과 0.03 이내의 오차를 지닌다고 말할 수 있다. (95% 의 신뢰도)

Series Navigation

<< 추정 (Estimation) – 일반적인 불편(unbiased) 점 추정량추정 (Estimation) – 신뢰구간 (Confidence Intervals) >>