조건부 확률은 아래와 같이 정의 된다.
P(B|A) = \dfrac{P( A \cap B)}{P(A)}
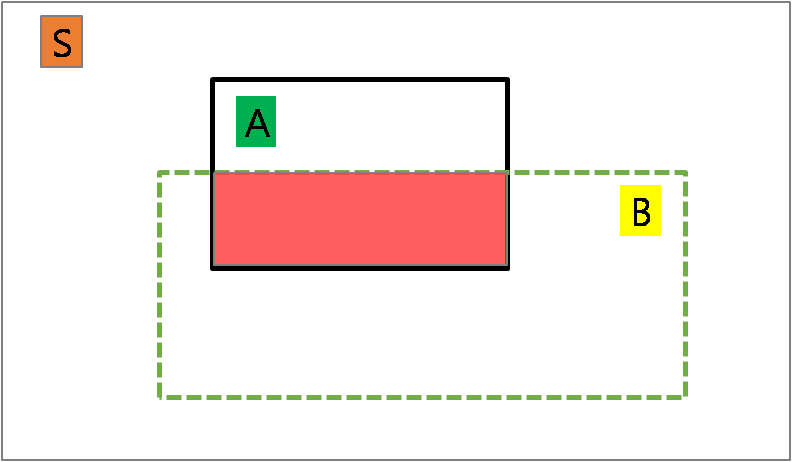
이것이 의미하는 바는 아래 그림 처럼 확률 공간이 먼저 A 로 정의된다는 것이다.
좀 더 부연하자면, P(B|A) 의 조건인 A 를 먼저 가정함으로써 전체 확률 공간 S 를
사용하는 것이 아니라, A 로 확률 공간을 좁히고 A 안에 있는 B 영역 A \cap B 의 확률을 구하게 되는 것이다.
조건부 독립의 의미를 이해하고, 독립적인 시행에 대해서 살펴보자.
상자에 7개의 검은공과 3개의 빨간 공이 있다고 가정할 때, 두 번의 시행으로 공을 뽑는 경우는 크게 두 가지 방법이 있겠다.
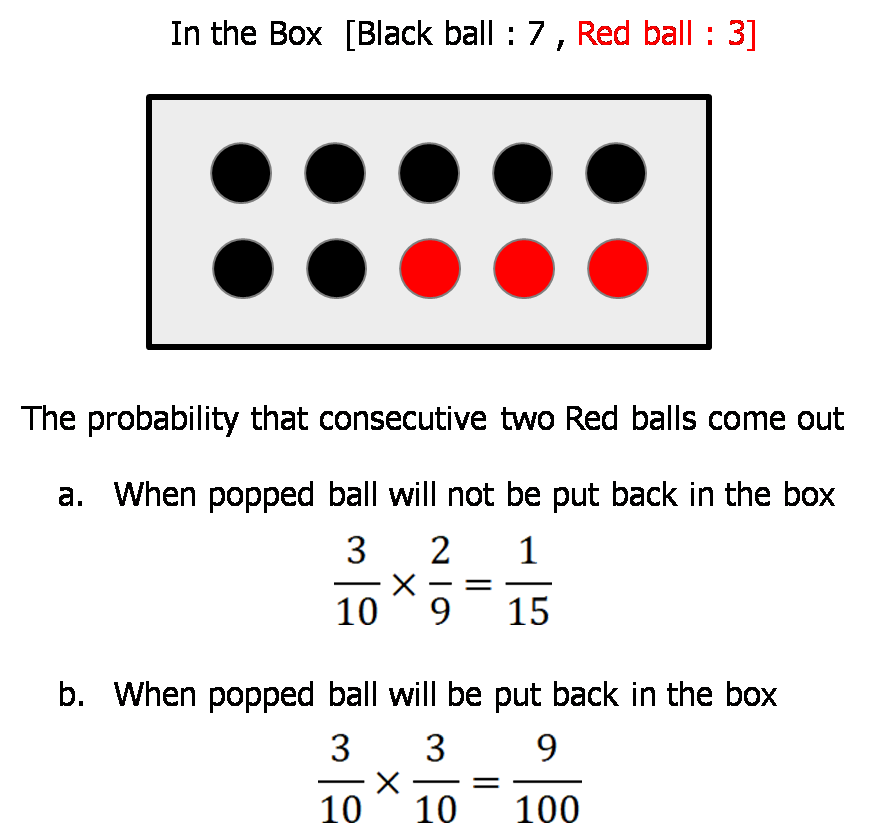
a. 의 경우는 뽑은 공을 다시 상자에 넣지 않는 경우이며,
b. 의 경우는 뽑은 공을 다시 상자에 넣는 경우다.
각각의 경우에 빨간 공이 2번 뽑힐 확률은 위와 같다.
이 때, 우리는 a. 의 시행은 서로 종속적이라고 부른다. 반면에 b. 의 시행은 서로 독립적이다.
이걸 확률식으로 표현해 보면,
(첫 번째 시행에서 빨간공이 나올 확률) * (첫 번째 시행에서 빨간공이 나왔을 때 두 번째 시행에서 빨간공이 나올 확률)
을 구하는 형태가 되겠다. 첫번째 뽑을 때, 빨간공이 나오는 사건을 A,
두번째 뽑을 때, 빨간공이 나오는 사건을 B 라고 하면
P(A) \times P(B|A)
이 예제를 써 놓고보니, 사건의 독립을 설명하기에 적합하지 않은데 그 이유는 여기 에서 설명하도록 하겠다.