이번 포스트에서는 추정(Estimation) 의 두 번째 포스트로 점 추정량의 편향과 MSE (The Bias and Mean Square Error of Point Estimators) 를 다룬다. 포스트의 내용은 『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.
2 . Bias 와 점 추정량의 MSE (Mean Square Error)
Bias 를 한글 용어로 ‘편향’ 이라고 하는데, 편의에 따라 Bias 와 편향을 혼용하여 사용하겠다. Mean Square Error 역시 ‘평균 제곱오차’ 라고 할 수 있는데 줄여서 ‘MSE’ 로 표현하기도 한다.
Bias 를 설명할 때 활을 쏘아 과녁에 맞힌다고 생각해 보자. (외서는 총이고 국내는 활을 예로 많이 든다.) 한번 활시위를 당겨 정중앙에 맞혔다고 했을 때, 다음번에도 정중앙에 맞힐 정도의 명궁이라는 보장을 할 수 있을까? 쉽게 결론 내릴 수 없는 건 한 번의 관측치로는 예측이 어렵기 때문이다. 여러번 쏘아 계속 정중앙에 맞힌다고 하면 비로서야 명궁으로 인정 할 수 있겠다. 일반적으로 추정값은 숫자이므로 관측 값들을 빈도로 표현하여 타켓 파라미터에 대해 얼마나 근접하게 군집을 형성하는지를 보고 추정량의 좋음 (goodness) 를 판단할 수 있다.
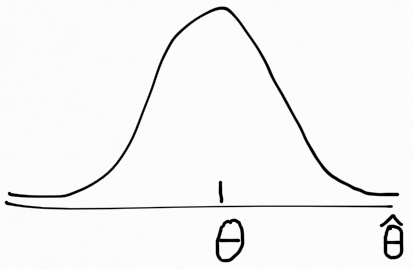
모집단 파라미터를 \theta 라 하고, 이에 대한 추정량을 \hat{\theta} 라 하자. 읽을 때는 ” \theta hat ” 이라고 읽는다. 아래 그림에서처럼 활쏘기 예제에서 타겟 파라미터에 대한 추정값의 분포 – 추정량의 표본 분포- 를 얻을 수 있다.
우리는 추정할 파라미터 값과 추정량의 평균이 같도록 만들고 싶다. 즉 E(\hat{\theta}) = \theta . 점 추정량이 이 식을 만족하면 비 편향 (unbiased) 되어 있다고 말한다.
| 정의.
\hat{\theta} 를 \theta 에 대한 점 추정량이라고 할 때, E(\hat{\theta}) = \theta 을 만족하면 \hat{\theta} 는 ‘불편추정량 ‘ (unbiased estimator) 이라고 한다. 반대의 경우, \hat{\theta} 는 편향(biased) 되어 있다고 한다. |
표본분포가 양의 값으로 편향되어 있는 경우 E(\hat{\theta})>\theta 이고 아래 그림과 같다.
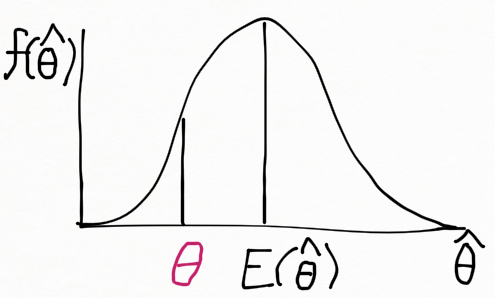
| 정의.
점추정량 \hat{\theta} 의 편향(bias) 은 B(\hat{\theta}) = E(\hat{\theta})-\theta 로 정의한다. |
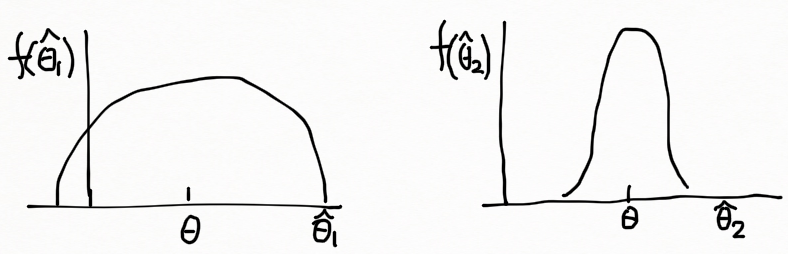
한편, 아래와 같이 불편 점추정량을 만족하는 두 가지 표본 분포를 살펴보면 오른쪽의 분포가 되는 것이 더 바람직하다. 그것은 반복되는 표본추출과정에서 \hat{\theta_2} 가 더 높은 비율로 모 파라미터 \theta 에 근접한 값들을 보유하기 때문이다. 따라서 unbiasedness 와 더불어 추정량의 분산, V(\hat{\theta}) 값도 가능한한 작은게 더 좋다.
편향(bias) 과 분산(variance) 대신에 타겟 파라미터와 추정량의 차이의 제곱의 평균을 새로운 기준으로 도입할 수 있겠다.
| 정의.
점 추정량 \hat{\theta} 의 mean square error 는 (\hat{\theta} - \theta)^2 의 기대값이다. MSE(\hat{\theta}) = E((\hat{\theta} - \theta)^2) |
MSE(\hat{\theta}) 는 \hat{\theta} 의 bias 와 variance 의 함수로 표현할 수 있다. 즉,
MSE(\hat{\theta}) = V(\hat{\theta}) + (B(\hat{\theta}))^2
※ 다음 성질을 이용하여 증명할 수 있다.
(\hat{\theta} - \theta) = [\hat{\theta}-E(\hat{\theta})]+[E(\hat{\theta})-\theta]=[\hat{\theta}-E(\hat{\theta})] +B(\hat{\theta})