가설검정 (Hypothesis Testing) – 통계 검정 결과를 보고하는 다른 방법: 유의수준 또는 p-value

 

 

 

 

 

이번 포스트는 가설검정의 다섯 번째 포스트로 통계 검정 결과를 보고하는 다른 방법: 유의수준 또는 p-value (Another Way to Report the Results of a Statistical Test: Attained Significance Levels or p-Values) 를 다룬다. 내용은『Mathematical Statistics with Applications, Sixth Edition, DUXBURY , Dennis D. Wackerly / William Mendenhall / Richard L. Scheaffer』 를 참고했다.

5. 통계 검정 결과를 보고하는 다른 방법: 유의수준 또는 p-value (Another Way to Report the Results of a Statistical Test: Attained Significance Levels or p-Values)

type Ⅰ error 의 확률 α 는 종종 ‘검정의 유의수준‘ 또는 간단히 ‘검정 수준‘ 이라고 불린다. 이 용어들은 다음과 같은데서 연유한다. 검정 통계량의 관측 값, 혹은 귀무 가설과 대립되는 어떤 값은 귀무가설을 기각할 수 있는 강력한 증거를 제시한다. 비록 작은 α 값이 추천되지만, 분석에 사용되는 α 값은 다소 임의적으로 선택할 수 있다. 어떤 실험자는 검정을 α = 0.05 로 할 수도 있으며 다른 실험자는 α = 0.01 을 선택할 수도 있다. 따라서 동일한 실험 데이터에 대한 두 실험자의 결론은 반대가 될 수 있다 – 한 사람은 귀무 가설이 α = 0.05 로 기각되어야 한다고 주장할 수 있고, 다른 한 사람은 α  = 0.01 로 기각되지 못한다고 말할 수 있다. 한편, α 값은 0.05 나 0.01 이 단지 관습적으로 사용되기도 하는데, 이는 단지 편의에 의한 것으로 type Ⅰ error 가 발생할 모든 영향도를 고려하지 않은 것이다. 한번 검정 통계량 (선거 예제에서는 Y 였고, 다(多) 표본 검정에서는 Z 였다.) 이 결정되면 ‘p-값’ 혹은 ‘획득된 유의수준’ 을 검정 결과로서 보고할 수 있다. 이 양은 ‘하나의 통계량으로서 귀무 가설을 기각 시킬 수 있는 가장 작은 α 값을 나타낸다.’

정의. W 를 어떤 검정 통계량이라고 할 때, ‘p-값’ 혹은 ‘획득된 유의 수준’ 은 관측된 데이터가 귀무가설을 기각시킬 수 있는 가장 작은 유의 수준 α 이다.

p-값이 작을 수록 귀무가설을 기각할 수 있는 증거는 강력해 진다. 많은 과학 학술지는 연구자들에게 p-값을 통계 검정결과와 함께 보고할 것을 요구한다. 왜냐하면 그럼으로써 독자들은 연구자가 선택한 α 값에 의해 귀무 가설이 기각되거나 기각되지 않은 것에 대해 더 많은 정보를 얻기 때문이다. 만약, 당신에게도 p-값이 충분히 작다면 귀무가설을 기각시킬 수 있을 것이다. 만약 실험자가 어떤 α  값을 염두해 두고 있다면, p-값을 α-level test 에 사용할 수 있을 것이다. ‘p-값은 귀무 가설을 기각 시킬 수 있는 가장 작은 α 값 이다.’ 따라서 상정한 α 값이 p-값 보다 크거나 같다면, 귀무 가설을 기각 시킬 수 있다. 실제로, p-값을 아래로 포함하고 있는 모든 α 값에 대해서 귀무가설은 기각된다. 반대로 α 가 p-값 보다 작다면, 귀무 가설은 기각될 수 없다. 그런 측면에서 볼 때, p-값은 출판된 연구에 대해 독자들이 관측 결과가 귀무가설에 대립하는(반대되는) 정도를 평가할 수 있도록 해 준다. 특별히, p-값은 독자들이 귀무가설을 기각해야 하는지 마는지 결정할 수 있는 α 값을 선택할 수 있는 권리를 준다.

검정에서 p-값을 찾는 과정이 아래 예제에 나와 있다.

예제. 앞 선 포스트들의 선거 예제를 살펴보자. n = 15 인 유권자 표본에 대해 H0: p= 0.5 versus Ha: p < 0.5 를 검정하려고 한다. Y 를 John 을 지지하는 유권자 수라고 할 때, Y = 3 에 대한 p-값을 확인하고 그 결과를 서술하라.

풀이.

앞선 예제에서 작은 Y 값에 대해서 H₀ 가 기각되었다. 이 검정에서 p-값은 다음과 같이 주어진다.

p-value = P\{Y \leq 3\} ,

여기서 Y 는 p = 0.5 이고 n = 15 인 이항분포를 갖는다. (아래 이항분포 그림에서 음영 영역이다. )

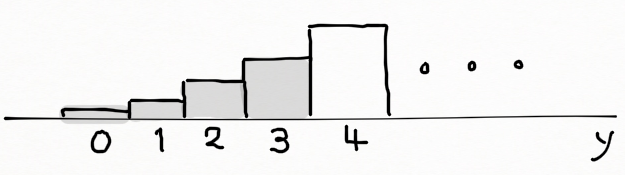
이항분포 확률을 구해보면, p-값은 0.018 이 된다.

p-값 0.018이 귀무가설을 기각하는 가장 작은 값을 나타내므로, 실험자가 α ≥ 0.018 을 선택하면 귀무가설을 기각하여 John 이 유권자들의 지지를 과반이상 확보하지 못하다고 얘기할 수 있을 것이고, 반대로 α 가 0.018 보다 작다면 귀무 가설을 기각하진 못한다.

 

위 예제는 검정 통계량이 이산 분포로 표현될 때, p-값을 포함하는 것이 특별히 유용하다는 것을 보여준다. 종종 이런 상황에서 특정 크기의 α 값을 만족하는 기각역을 찾지 못하는 경우가 있는데 예를 들면, 위 예제의 경우에 α = 0.05 을 만족하는 \{y \leq a \} 형태인 기각역을 찾을 수가 없다. 이와 같은 경우는,  검정 통계량을 나타내는 이산확률분포를 기준으로 얻어지는 α 값을 한정하기  위해 p-값을 보고하는 것이 더 선호된다. 또한, 위의 예제는 p-값을 계산하는 일반적인 방법을 알려준다. 만약 검정 통계량 W 보다 작은 값에 대해 대립가설 H_a 를 지지하고, 귀무가설 H₀ 를 기각한다면, RR: \{w \leq k \} 이고 관측된 w_0 에 대해 p-값은 다음과 같다.

p-값 = P(W \leq w_0, ~when~ H_0~ is~ true)

 

마찬가지로, 검정 통계량 W 보다 큰 값에 대해 대립가설 H_a 를 지지하고, 귀무가설 H₀ 를 기각한다면, RR: \{w \geq k \} 이고 관측된 w_0 에 대해 p-값은 다음과 같다.

p-값 = P(W \geq w_0,~ when~ H_0~ is~ true)

 

two-tailed 인 경우의 p-값 계산은 아래 예제를 살펴보자.

예제. 다(多) 표본 검정 포스트의 예제3. 에서 통계 검정의 p-값을 구하라.

풀이.

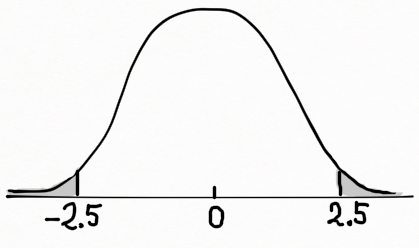
위 그림의 음영 영역의 면적이 p-값을 나타낸다.

앞의 예제에서 귀무가설 H₀ : (\mu_1 - \mu_2) =0 에 대해 대립가설 Ha : (\mu_1 - \mu_2) \not= 0 였다. 검정 통계량은 앞 선 예제에서 계산한 결과 z = -2.5 였다. 양측 검정 (two-tailed test) 이므로 p-값은 Z ≤ -2.5 와 Z ≥ 2.5 의 확률을 더한 값이다. P(Z ≤ -2.5) = P(Z ≥ 2.5) = 0.0062 이므로 p-값 = 2 ( 0.0062) = 0.0124 이다. 따라서 만약에 α = 0.05 라면 H_a 를 지지하고, 귀무가설 H₀ 를 기각할 수 있고, 이는 앞 선 예제의 결론과 같으며 남·녀 사이의 평균 반응 시간에 차이가 있다는 걸 입증한다. 하지만 α = 0.01 이라면 두 성별 간의 반응시간에 차이가 있다고 인정할 수 없을 것이다.

 

연구자가 검정의 p-값을 보고하고 그 해석을 독자에게 남기는 것은 전통적인 통계 검정 절차를 어기는 것은 아니다. p-값을 보고하는 것은 단순히 귀무 가설을 기각하느냐 (type Ⅰ error 와 type Ⅱ error 를 범할 가능성과 함께)에 대한 결정을 독자에게 남기는 것이다. 따라서 α 값을 선택하는 책임과 가능한 경우, type Ⅱ error 를 유발하는 β 확률을 계산해 보는 문제는 독자에게 전가되는 것이다.

Series Navigation

<< 가설검정 (Hypothesis Testing) – 가설검정절차와 신뢰구간사이의 관계가설검정 (Hypothesis Testing) – 가설 검정의 이론에 대한 추가 설명 >>