QQ Plot

Q-Q (quantile-quantile) Plot

Q-Q Plot 을 살펴보기 이전에 먼저 Quantile 이라는 개념을 짚고 넘어가자. Quantile 은 분위수라는 개념인데, 데이터들을 정렬한 뒤에 몇 등분으로 나눌 수 결정하고, 나눠진 등분을 구분하는 구분자를 찾는 개념이다. 이는 ‘Quantile (분위수)‘ 포스트를 참고하길 바란다.

Q-Q 가 의미하는 바가 quantile-quantile 인데,

Theoretical-Quantile vs. Emprical-Quantile ( Sample-Quantile )

로 생각하면 된다. 즉 가로축에는 이론상의 Quantile 을, 세로축에는 획득된 샘플 값의 Quantile 을 찍었을 때 이론과 실제가 얼마나 차이나는지를 쉽게 표현하기 위한 Plot 이다. (물론 가로, 세로가 바뀔 수도 있다.)

일종의 Q-Q Plot 인 Normal Probability Plot 을 예로 들어서 계속 설명하겠다.

유투브에 엑셀로 쉽게 설명한 영상이 있어 이를 참고하였다.

어떤 중학교 남학생의 키 데이터를 생각해 보자. 데이터를 키의 오름차순으로 정리한 후 개수만큼 인덱스를 정한다. 여기에는 57개의 데이터가 있다. 각각의 데이터의 이론적인 quantile (theoretical quantile) 인, 57-quantile 을 (i-0.5)/57 로 근사하여 계산한다. 그 후에 실제 데이터는 Standard Normal Distribution (정규 노멀 분포) 를 가정하여 정규화 시킨다. ( Z = \dfrac {(x-\mu)}{\sigma} )

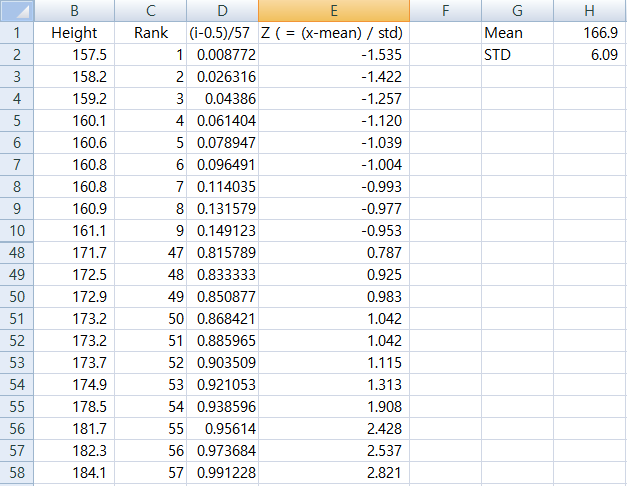
Theoretical Quantile 을 가로축에 Empirical Quantile 을 세로축에 놓고 그래프를 그리면 Q-Q Plot 이 그려진다. (여기서 모집단의 분포를 모르지만 이론적인 분위수를 1부터 57까지 누적정규확률분포에 근사한다.)

 

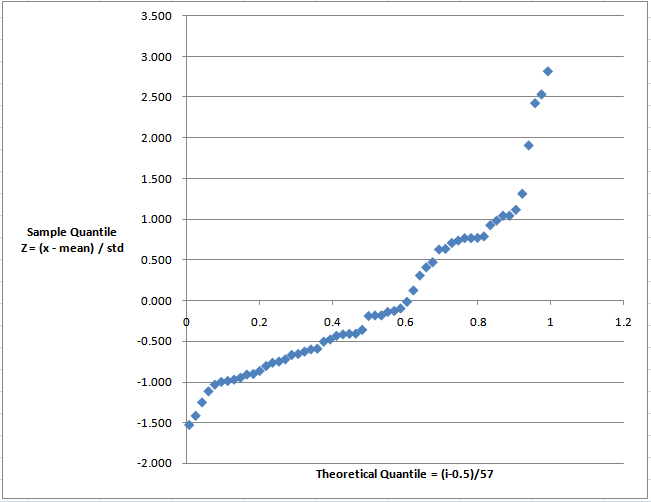
QQPlot 의 형태

이론적 분위수 (Theoretical Quantiles) 와 실제 관찰된 분위수 (Empirical Quantiles) 를 Plotting 해보면, 대략적인 확률분포 형태를 짐작 해 볼 수 있다.

① 정규분포 (Normal Distribution) 을 따를 때

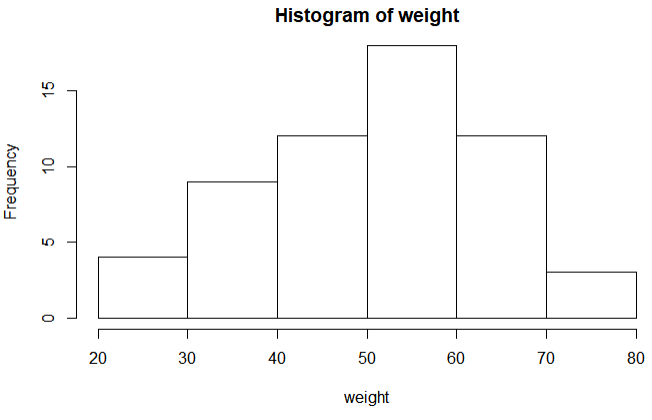
먼저 정규분포와 가깝게 데이터를 생성해 보면 다음과 같은 정규분포와 근접한 히스토그램을 얻을 수 있다.

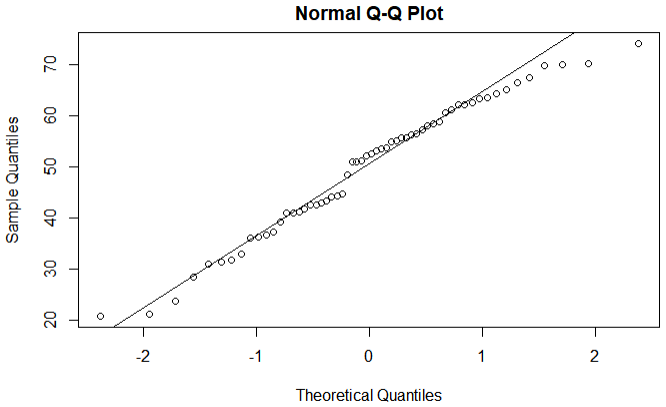
위 데이터로 QQPlot 을 그려보면 이론적인 정규분포의 Quantile 값과 거의 일치하여 직선으로 Fitting 되는 것을 확인 할 수 있다.

② 왼쪽으로 치우친 분포 (Left-Skewed  Distribution) 을 따를 때

분포가 왼쪽으로 치우치도록 데이터 샘플링 확률을 변경하여 히스토그램을 그려보면 다음과 같다.

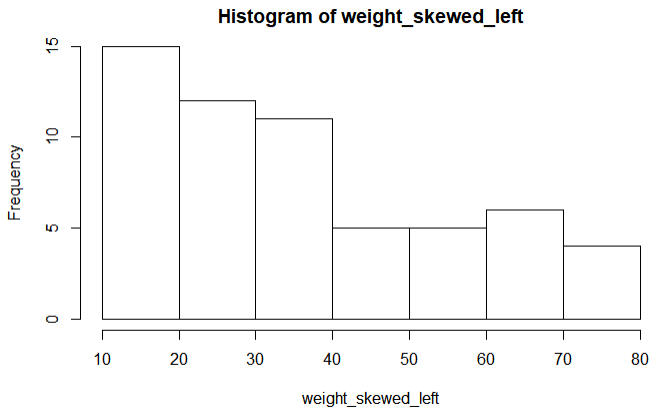
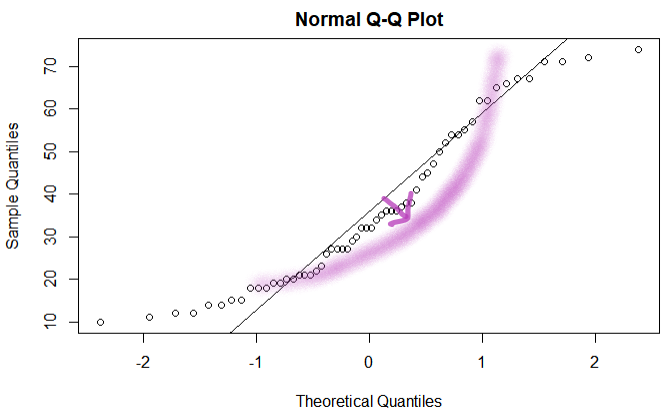
위 히스토그램의 QQPlot 을 그려보면 아래와 같이 이론적인 Quantile 값에 비해 아래로 불룩한 형태로 그려지게 된다. 아래에서 좀 더 살펴보겠지만 같은 Q_t 값에 비해 Q_e   값이 작기 때문으로 생각할 수 있다.

③ 오른쪽으로 치우친 분포 (Right-Skewed  Distribution) 을 따를 때

분포가 오른쪽으로 치우치도록 데이터 샘플링 확률을 변경하여 히스토그램을 그려보면 다음과 같다.

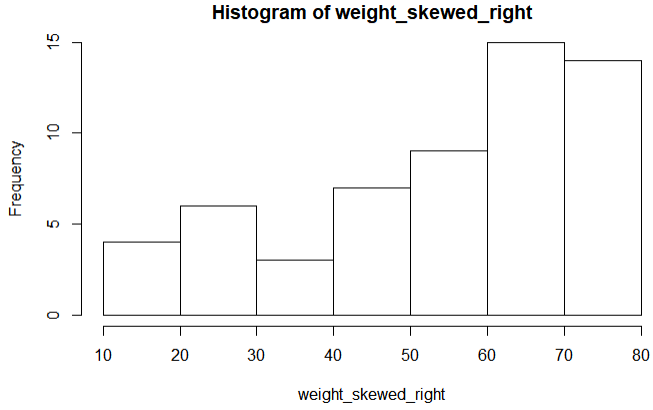
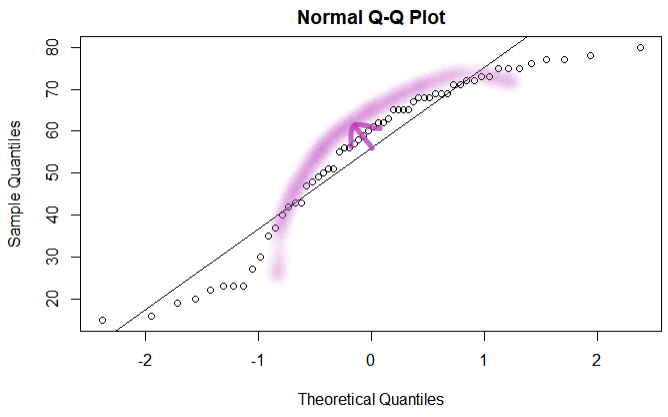
이번엔 QQPlot 은 이론적인 Quantile 값에 비해 위로 불룩한 형태로 그려지게 된다.

위에 사용된 R 소스는 GitHub 에 공유하였다.

 

QQPlot 의 해석

먼저 이곳의 해석을 참조 했음을 밝혀둔다.

Q_t 를 Theoretical Quantile 로, Q_e 를 Empirical Quantile (또는 Sample Quantile) 로 지칭하자. 아래와 같이 표본 분포(Sample Distribution) 가 Light-Tailed (이론적인 분포에 비해 꼬리 값이 더 얕은 분포) 를 가질 경우,

 

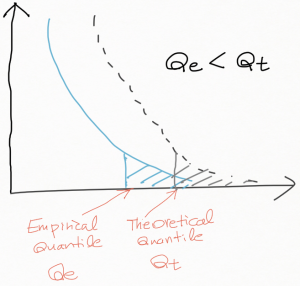
Q_e < Q_t 를 만족하게 된다. 반대로 Heavy-Tailed (이론적인 분포에 비해 꼬리 값이 더 두터운 분포)인 경우는  Q_e > Q_t 이 되고, 이를 그림으로 표현해 보면 아래와 같다.

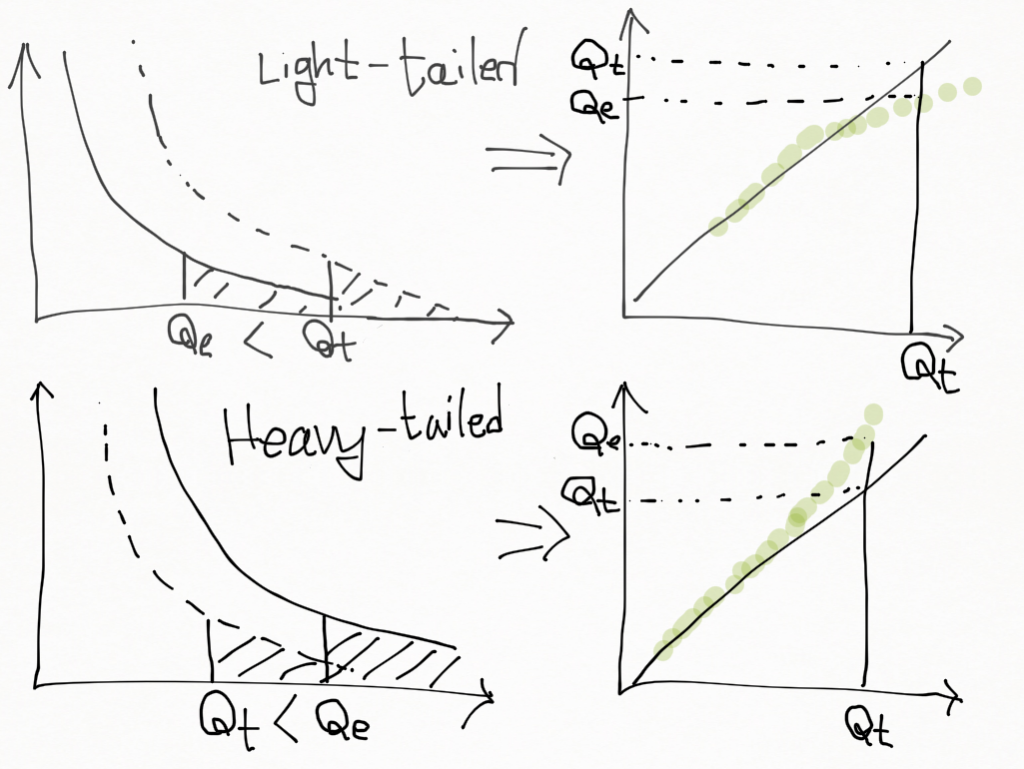
즉, Light-Tailed 의 QQPlot 의 경우 직선 아래로 쳐지게 되며, Heavy-Tailed 의 QQPlot 의 경우 직선 위로 치솟게 되는 형태가 된다.

Left-Skewed 와 Right-Skewed 분포는 어떻게 될까? Left-Skewed 의 경우 분포가 왼쪽으로 치우치게 되어 정규 분포에 비해  Q_e < Q_t 관계가 되어 가운데가 아래로 불룩한 형태로 QQPlot 이 그려지며, Right-Skewed 분포는 반대로 가운데에서 위로 불룩한 형태가 된다. (위의 R Plot 을 확인해 보자.)

양쪽 꼬리 각각 (Right Tail 과 Left Tail)의 Light-Tailed 형태와 Heavy-Tailed 형태의 조합에 대해 정리해 보면 아래와 같이 정리할 수 있겠다. 4가지 조합이 나오며 Right Tail 의 형태가 QQPlot 의 오른쪽부분, Left Tail 의 형태가 왼쪽 부분의 모양을 결정한다.

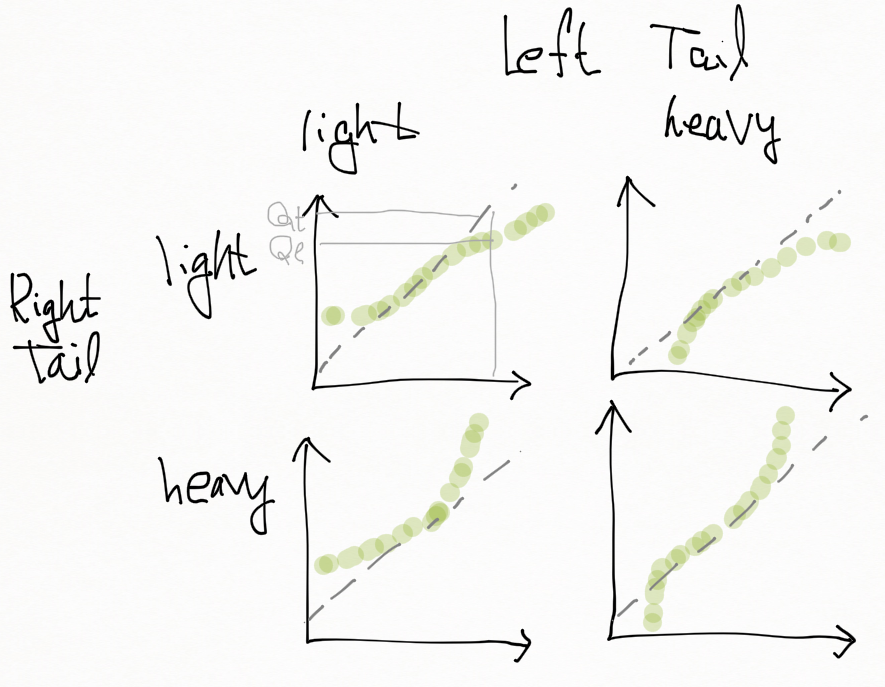
위 링크에서도 소개 되었지만 MOOC 의 MIT 강의에서 이를 잘 설명해주고 있다. (45분 경)

 

이번 포스트에서 강조하고 싶은 부분은 이론적인 분위수(Theoretical Quantile)과 실제관찰된 분위수(Empirical Quantile) 간의 비교를 통해서 QQPlot 을 해석하면 된다는 것이다. 위 설명이 도움이 되었길 바라며, 포스트를 마친다.