조건부 독립 ( Conditional Independence )

조건부 독립에 대해 생각해 보자. 많은 머신러닝 책들에 보면 베이즈 정리와 함께 조건부 독립에 대해서 장황하게 설명한 내용들이 많은데, 아래 그림 만큼 쉽게 와 닿는 예제도 없는 듯하다. 온라인에 공개된 KAIST 문일철 교수님의 머신러닝 강좌(3-2) 의 강의노트에서 발췌한 그림을 보기로 하자.

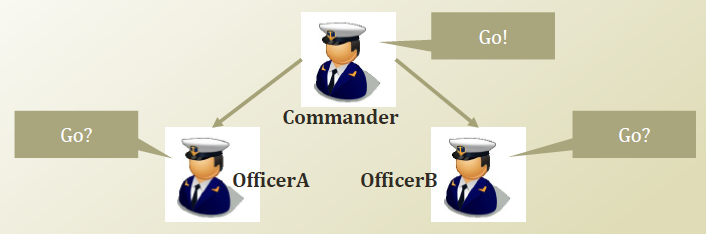
명령을 내리는 상사와 부하직원 2명이 있다고 가정해 보자. 만약 OfficerA 가 OfficerB 가 앞으로 가는 것을관찰했다고 치면 OfficerA 는 OfficerB 가 상사로부터 명령을 전달받고 움직이고 있다고 생각할 수 있다.

이 때 OfficerA 가 앞으로 갈 확률을 생각해 보자. 그 확률은 OfficerB 가 앞으로 가고 있는걸 보지 못했을 때 확률보다는 작을 것이다. (조직 사회의 특성을 생각해 보자)

따라서, P(OfficerA \, = \, Go \, | \, OfficerB \, = \, Go)\, > \, P(OfficerA\, = \, Go)

위는 Marginal Independence 가 성립하지 않음을 보여준다. 흔히 A, B 사건이 독립이라고 말할 때 Marginal Independence 를 말하는데 두 사건 (OfficerA 가 앞으로 가는 사건과, OfficerB가 앞으로 가는 사건) 은 서로 독립이 아니라고 할 수 있다.

상사가 ‘앞으로 가!’ 라고 명령을 내린 상황에선 어떠한가?

이 경우 OfficerA 는 OfficerB 가 앞으로 가고 있는 것을 보고 있었을지라도 상사가 가라고 이미 명령했다는 사실을 알고 있기 때문에 OfficerB 가 앞으로 가고 있다는 사실과 관계없이 앞으로 가게 된다. 이 경우 OfficerB 가 앞으로 가고 있다는 사실은 상사의 명령을 전달 받은 OfficerA 입장에서 영향을 미치지 않는 정보가 되고 우리는 이것을

조건부 독립 ( Conditional Independence )

이 성립한다고 얘기할 수 있다. 즉,

P(OfficerA\, = \, Go\, | \,OfficerB\,=\,Go, Commander\, = \, Go(Yawl))
=P(OfficerA\,=\,Go\, | \, Commander\,=\,Go)

 

엄밀하게 조건부 독립에 대해서 정의해 보면,  [강의노트]

x_1 is conditionally independent of x_2 given y

(\forall x_1,x_2,y) \, P(x_1|x_2,y)=P(x_1|y) \cdots (*)

그리고 아래의 딸림 정의를 유도할 수 있다.

P(x_1, x_2|y) = P(x_1|y) \cdot P(x_2|y)

 

딸림 정의를 유도해 보자.

From the (*),

P(x_1|x_2,y)= \dfrac {P(x_1, x_2, y)}{P(x_2,y)} = P(x_1|y)

 

\Longrightarrow P(x_1,x_2,y) = P(x_2,y) \cdot P(x_1|y)

 

\Longrightarrow P(x_1,x_2,y) = P(x_2|y) \cdot P(y) \cdot P(x_1|y)

 

이미 P(x_1,x_2|y)= \dfrac {P(x_1,x_2,y)} {P(y)} 을 알고 있으므로

\therefore P(x_1,x_2|y) = P(x_1|y) \cdot P(x_2|y)