이 Post 는 Coursera 강의 “Bitcoin and Cryptocurrency Technologies” 와 해당 강의 저자의 draft 를 참고하여 작성된 것입니다.
좀 더 쉬운 이해를 위해 zhaohuabing.com 블로그의 일부 그림을 차용하였습니다.
(For more easy understanding the concept of hash pointer and data structures, I used some images at zhaohuabing.com blog )
Lecture 1.2 Hash Pointers and Data Structures
[Hash Pointer]
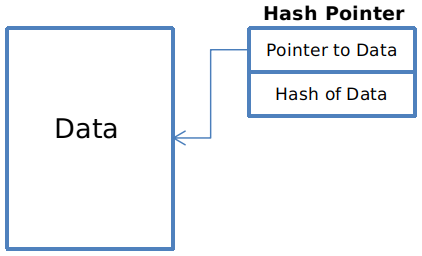
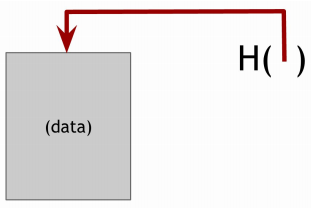
일반적인 Data Pointer 의 경우, Data 의 주소를 가리킨다. 이에 반해 Hash Pointer 는 데이터의 주소는 물론이고 Data 의 Hash 값을 포함한다. 따라서 Hash Pointer 로 정보의 변경이 일어났는지를 판단할 수 있다.
[블럭 체인 : Block Chain]
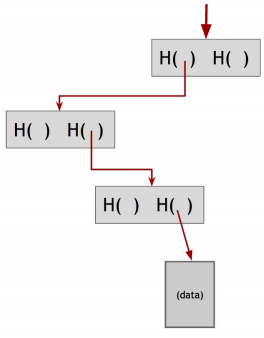
블럭 체인 데이터 구조에 사용된 Hash Pointer 를 살펴보자.
일반적인 Linked-List 구조에서는 하나의 노드가 데이터와 이전 노드를 가리키는 Pointer 로 구성되어 있는 것에 반해서 Block Chain 구조에서는 이 Pointer 가 Hash Pointer 로 대체 된다. (아래 그림 참조)
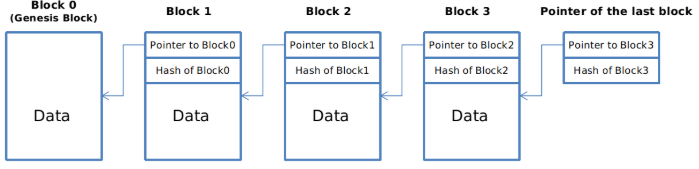
따라서 Hash Pointer 는 이전 블럭의 데이터뿐 아니라 이전 블럭이 변경 (변조) 되지 않았다는 것을 증명시켜 준다. 하나의 Use-Case 로 변조방지 로그 (temper-evident log) 의 경우를 살펴보자.
[변조방지 로그 : temper-evident log]
연속적으로 쌓이는 로그와 같은 긴 데이터를 저장할 데이터 구조를 생각해 보자. 계속적으로 로그를 덧붙여 쌓는 방식이다. 그런데 만약 누군가 의도적으로 앞선 데이터를 변경한다고 할 때 그것을 탐지하고 싶다.
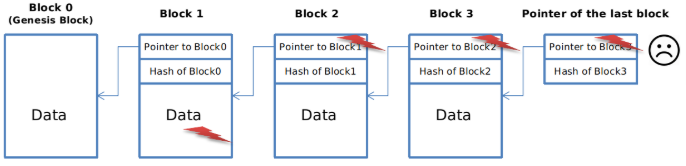
우리는 체인의 마지막 블럭의 Hash Pointer 만 알고 있으므로, 침입자의 목적은 들키지 않고 블럭체인의 중간에 있는 어떤 데이터를 변경하는 것이다. 이 목적을 달성하기 위해 중간의 k 번째 블럭의 데이터를 변경했다고 하자. 이럴 경우 k+1 번째 블럭의 Hash Pointer 안에 저장된 k 번째 블럭의 Hash 값은 이전과 일치하지 않기 때문에 우리는 쉽게 변경을 발견할 수 있다. 침입자는 연속적으로 k+1번째 Hash Pointer 를 변경하려 할 것이다. 하지만 이 경우에도 k+1 번째 블럭은 Hash Pointer 와 Data 를 포함하고 있으므로 k+2 번재 블럭의 Hash Pointer 가 가진 Hash 값은 이전과 일치하지 않게 된다. 연속적인 변경으로 최종 블럭까지 변경을 할 경우에는 우리가 갖고 있는 마지막 Hash 값과 일치하지 않기 때문에 결국은 잡히게 된다!
[Merkle trees]
또 다른 유용한 데이터 구조는 Hash Pointer 를 binary tree 로 엮은 구조로 Merkle tree 라 불린다. 데이터를 포함한 블럭들은 tree 의 leaf 에 달려 있고, 두 개씩 그룹지어서 각각의 Hash Pointer 를 가진 줄기 (노드) 를 구성한다. 최종적으로 최상위에는 2개의 Hash Pointer 를 갖는 Root 노드가 위치한다.
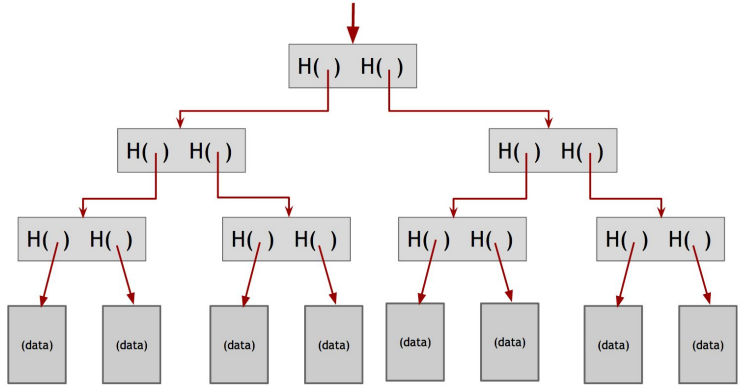
tree 를 통해서 탐색이 가능한 점과 블럭 체인에서 가능했던 temper-evident 도 가능하다. (왜냐하면 상단에서부터 데이터 블럭까지 전파 되기 때문에)
① Proof of membership :
블럭 체인과 달리, Merkel tree 에서는 데이터 블럭이 tree 에 속해 있는지 증명하기 위해서, 단지 데이터 블럭에서부터 root 까지의 거슬러 올라갈 수 있다는 (경로) 것을 보여주면 된다. log(n) time
② sorted Merkle tree :
leaf 에 있는 데이터블럭들을 sorting (정렬) 한 것을 ‘sorted Merkle tree’ 라고 한다.
③ Proof of non-membership :
‘sorted Merkle tree’ 를 활용하면 쉽게 non-membership 을 밝혀낼 수 있다. 찾고자하는 item 이 있는 바로 이전의 (sorting order 기준) 데이터 블럭의 경로를 확인하고 바로 이후의 데이터 블럭의 경로를 확인한다. 만약 두 개의 데이터 블럭이 연속적으로 ‘sorted Merkle tree’ 에 위치해 있다면 확인하는 item 은 ‘sorted Merkle tree’ 의 member 가 아니다.
[Cyclic , Directed-Acyclic]
앞에서 블럭 체인과 binary tree 구조에서 Hash Pointer 가 사용된 것을 확인 할 수 있었다. 일반적으로는 순환하는 (cyclic) 데이터 구조를 제외한 pointer-based 데이터 구조에서는 Hash Pointer 를 사용가능하다. 비순환 (acyclic) 구조에서는 Hash Pointer 를 갖지 않는 블럭에서부터 시작해서 이후 구조로 이어질 수 있다. 반면, 순환 (cyclic) 데이터 구조에서는 시작과 끝이 없으므로 Hash Pointer 를 적용할 수 없다.
특이한 점은 방향성 있는 비순환 구조 (Directed-Acyclic)에서는 membership 관계를 아주 효율적으로 계산할 수가 있다. 향후 강의에서 이 부분들을 확인 할 수 있을 것이다.