Lecture 1.1 Cryptographic Hash Functions

• 이 Post 는 Coursera 강의 “Bitcoin and Cryptocurrency Technologies” 와 해당 강의 저자의 draft 를 참고하여 작성된 것입니다.

Lecture 1.1 Cryptographic Hash Functions

<Hash Function 의 특징>

• 어떤 크기의 어떤 종류의 문자열도 Input 이 될 수 있다.
• 고정된 크기의 Output 을 생성한다. (강의에서는 256 bit 를 가정)
• Hash Function 을 효율적으로 계산가능하다.

Hash Function 이 암호화폐에 사용되기 위해서는 다음의 세 가지 특성을 추가적으로 만족해야 한다.

1. 충돌  저항성 (Collision-resistance)
2. 숨김 (Hiding)
3. Puzzle-friendliness (번역하기 어려워 원문 내용을 그대로 사용 함)

순서대로 확인해 보겠다.

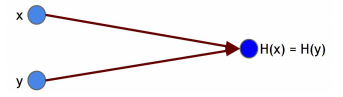
1. 충돌 저항성  (Collision-resistance)

어떤 Hash Function 이 충돌 저항성을 지녔다는 것은, H(x) = H(y) 이면서 x ≠ y 를 만족하는 두 값 x, y 를 찾기 불가능하다는 것이다.

Input 에 비해 Output 의 경우의 수가 적기 때문에 적어도 Output 값 하나에 적어도 하나 이상의 Input 이 대응되는 경우는 반드시 존재하게 된다. (비둘기 집의 법칙 : Pigeonhole Principle)

가능한 Input 의 수는 가능한 Output 의 수 보다 많기 때문에 필연적으로 충돌은 더 존재한다. 하지만 누구도 그 충돌을 발견하기는 어렵다. 좀 더 확실히 하기 위해서 Input 의 개수를 2²⁵⁶ +1 개로 한정하고 이들의 Hash 값 중 2개의 값이 중복되는지 체크해 보는 실험을 한다고 가정해 보자.

만약, 우리가 랜덤하게 Input 값을 선택하여 Hash 값을 계산한다면 2²⁵⁶+1 개를 모두 계산할 필요는 없을 것이다. 사실은 2¹³⁰+1 개의 랜덤 Input 에 대해서 99.8% 의 확률로 중복은 발생한다. (Birthday Paradox) 하지만 이 정도를 계산하는데 얼마만큼의 연산 시간이 소요되는가? 천문학적인 시간이다. 지금까지 지구상에 만들어진 모든 컴퓨터를 동원해 우주가 탄생했을 때부터 계산하더라도 그 충돌을 발견할 확률은 지극히 작다. 당장 2초 뒤에 지구가 소행성에 부딪혀 산산조각날 확률 만큼이다.

그렇다면 Hash Function 은 충돌에 항상 자유로울까?

H(x) = x mod 2²⁵⁶ 과 같이 마지막 256 자리에 대해서 같은 결과를 주는 경우 아주 쉽게 충돌을 찾을 수 있다. 3 과 2²⁵⁶+3 같이 말이다. 따라서 일반적으로 Hash Function 이 Collision-resistant 한걸 증명할 수는 없다. 하지만 우리가 암호화폐에 사용하는 Hash Function 에 대한 충돌을 찾는 것은 매우 어렵다. 일부 MD5 같은 Hash 의 경우 수 년간의 노력 끝에 충돌방법을 찾았고, 결국 폐기 되었다.

[응용 : 메시지 요약]

H(x) = H(y) 이면 x = y 임을 충분히 믿을 수 있을 때 메시지를 저장할 필요없이 Hash 값만 저장해서 분류할 수 있다.

 

2. 숨김 (Hiding)

어떤 비밀 값 r 이 high min-entropy 를 갖는 확률 분포에서 선택되고, H( r || x ) 가 주어졌을 때 x 를 찾는 것이 불가능하다면, Hash Function, H 는 숨김 (Hiding) 가능하다.

이 섹션에서는 Commitment (잠금 / 계약) 의 응용방식에 대해서 살펴보자.
※ Commitment : 잠금, 계약으로 번역했다.

[응용 : 계약/잠금]
* draft 에서는 API 시그니처가 Coursera 강의와 달라 여기서는 Coursera 강의를 기준으로 설명한다.

“어떤 값을 봉투 (Envelope) 에 봉인” 하고, 나중에 “그 봉투를 열어” 보고 싶다. 즉, “Commit to a value, reveal it later”

1) Commit (잠금) (com, key) := commit(msg) key 값과 함께 message 를 commit 하면 commitment 와 key 값을 리턴 받는다. 구현방법 : commit(msg) := ( H(key | msg), key ) * key 는 랜덤 256-bit 값 publish : com

용어들은 다음과 같이 해석할 수 있다.

“Commitment” = “Envelope (봉투)”
“Key” = “봉투를 열기 위한 열쇠”
“Publish” = “봉투를 테이블 위해 놓아 모든 사람이 볼 수 있게 하는 것”

 

2) Verify (검증) match := verify(com, key, msg) commitment 와 key, message 를 Input 으로하여 검증결과를 리턴 받는다. 구현방법 : verify(com, key, msg) := ( H(key | msg) == com ) publish : key, msg

“commitment 결과와 key 값, message 를 통해서 검증할 수 있다.”

 

<보안 속성>

① 숨김 (Hiding) : 봉투 (Envelope) 를 알더라도 속의 값 (value) 를 알 수 없다.
=> H(key | msg) 가 주어졌을 때, message 를 알아 낼 수 없다.

H(key | msg)  : key 값과 message 를 연결한 것을 Hashing 했다는 의미
* key | msg 의 의미 = (문자열끼리) 연결되었다는 의미 (concatenated)

 

② 묶임 (Binding) : 봉투 (Envelope) 안에 있는 값을 Commit 했을 때, 나중에 그걸 다시 변경할 수 없다.

즉, 서로 다른 message 끼리는 verify 한 결과가 참일 수 없다는 뜻이다.

• infeasible to find msg != msg’ such that verify( commit(msg), msg’ ) == true
• Infeasible to find msg != msg’ such that H(key | msg) == H(key | msg’)

위에서 알아본 개념대로 특정 메시지 (message) 와 함께 넓게 퍼진 분포 (very spread out distribution) 에서 선택된 key 값 (256-bit) 을 봉투에 봉인 (commit) 하는 절차를 Hashing 이라고 할 수 있고, commit 된 후의 봉투 안의 내용은 볼 수 없으므로 ‘숨김 (Hiding) 속성’ 의 정의와 일치하는 것을 알 수 있다. 이것은 또안 Collision-Free 속성을 만족시킨다.

 

3. Puzzle-friendliness

의미 :

“모든 가능한 Output 값 y 에 대해서, k 가  ‘high min-entropy’ 를 갖는 분포의 값이라면 H(k | x) = y 를 만족하는 x 를 찾는 것은 불가능하다.”

[응용 : 계약/잠금]

‘puzzle ID’ ( ‘high min-entropy’ 를 갖는 분포의 값 ) 와 타겟 집합 Y 가 주어졌을 때, H (id | x) ∈ Y 를 만족하는 ‘Solution’ x 를 찾는 특정한 방법은 없다.

 

<Specific Hash function SHA-256>

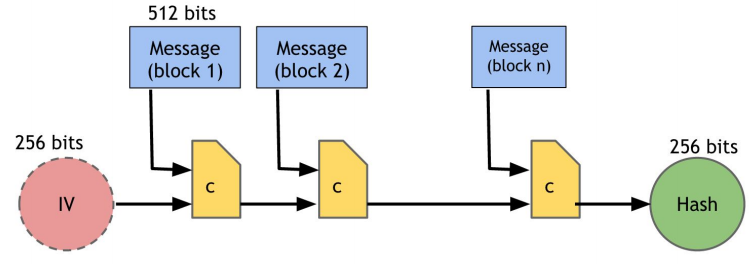
암호화폐에 일반적으로 사용되는 SHA-256 Hash Function 에 대해 살펴 보자. 첫 번째 블럭은 256-bit 의 ‘IV’ 로 표현되는 Initialization Vector (IV) 이다. 뒤에 512-bit 의 메시지 블럭과 결합되는데 압축 함수 ( Compression Function ) 의 결과와 다음 메시지 블럭이 순차적으로 결합하면서 연결되는 구조이다. 마지막 메시지 블럭은 512-bit 보다 작을 수 있으므로 여유 bit 를 채운다. 최종적으로 얻은 결과가 256-bit 의 Hash 값이 된다.