2020 한국인공지능학회 동계강좌 정리 – 5. AITrics 이주호 박사님, Set-input Neural Networks and Amortized Clustering

2020 인공지능학회 동계강좌를 신청하여 2020.1.8 ~ 1.10 3일 동안 다녀왔다. 총 9분의 연사가 나오셨는데, 프로그램 일정은 다음과 같다.

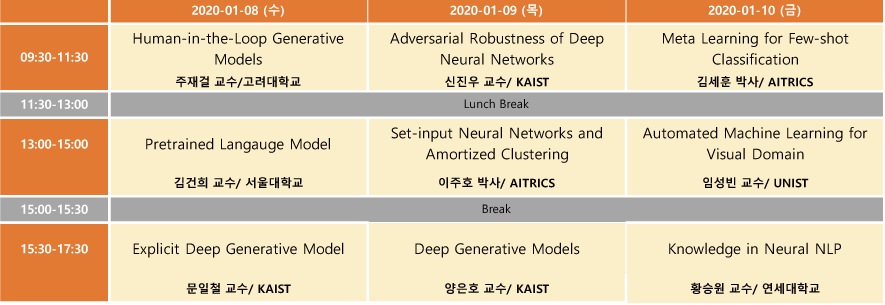
전체를 묶어서 하나의 포스트로 작성하려고 했는데, 주제마다 내용이 꽤 많을거 같아, 한 강좌씩 시리즈로 묶어서 작성하게 되었다. 다섯 번째 포스트에서는 AITrics 이주호 박사님의 “Set-input Neural Networks and Amortized Clustering” 강연 내용을 다룬다.

1. Introduction
   1. Common assumption
      • Typical machine learning algorithms act on fixed dimensional data
      • How about RNN ?
        • Maybe variable-length, but in fixed-order (order matters)
        • Repeated application of neural networks for fixed-length inputs
   2. Challenging tasks
      • Point-cloud classification
      • Multiple instance learning
      • Few-shot image classification
   3. Set-input problems
      • Inputs
        • variable length
        • order does not matter
        • In other words, inputs are sets.  X = \{ x_1, ..., x_n \}
      • Today’s topic
        • y = f(x;\theta)
        • \theta* = arg min E_{p(x,y)}[L(f(x;\theta),y)]
2. DeepSets
   1. Permutation invariance and equivariance
      • A function f: 2^x \rightarrow y is permutation invariant if
        f(x_1, ..., x_n) = f(x_{\pi(1)}, ..., x_{\pi(n)})
      • A function f: x^n \rightarrow y^n is permutation equivariant if
        f(x_1, ..., x_n)=[f_1(x_1, ..., x_n), ..., f_n(x_1, ..., x_n)],
        f(x_{\pi(1)}, ..., x_{\pi(n)})= [f_{\pi(1)}(x_1,..., x_n), ..., f_{\pi(n)}(x_1, ..., x_n)]
   2. DeepSets
      • Zaheer et al, Deep Sets, NIPS 2017
      • Wagstaff et al, On the Limitations of Representing Functions on Sets, arXiv 2019
        
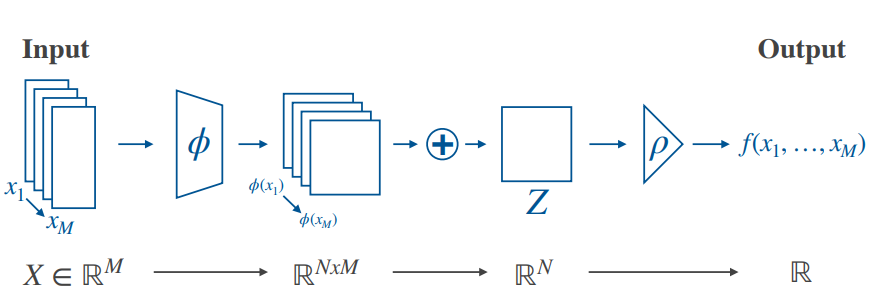
      • \rho and \phi : any feedforward neural network
        f(x) = \rho(\sum_{x \in X} \phi(x))
      • Are DeepSets expressive enough?
        • Let f:2^x \rightarrow y be a function on a countable x Then f is permutation invariant if and only if it is sum-decomposable [Zaheer et al, 2017]
        • If x is uncountable, then there exists a function 2^x \rightarrow R which are not sum-decomposable [Wagstaff et al, 2019]
        • Let f: R^{\leq n} \rightarrow R be a continuous function. Then f is permutation-invariant if and only if it is sum-decomposable with \phi(\cdot) \in R^n
   3. Examples for DeepSet-like architectures
      1. Prototypical networks
         • Snell et al, Prototypical Networks for Few-shot Learning, NIPS 2017
      2. Neural statistician
         • Edwards and Storkey, Towards a Neural Statistician, ICLR 2017
      3. Neural process
         • Garnelo, Neural Processes, ICML 2018
           • Can we learn everything from data, without assuming Gaussianity?
      4. PointFlow
         • Yang et al, PointFlow: 3D Point Cloud Generation with Continuous Normalizing Flows, ICCV 2019
   4. Limitations of DeepSets
      1. Sum-decomposition does not take into account the interactions between elements in a set
      2. One can easily think of a problem that modeling interactions between elements is crucial
3. Amortized clustering
   1. Clustering methods
      • K-means clustering, spectral clustering, hierarchical clustering
      • Soft K-means, Mixture of Gaussians
      • Randomly initialize and iteratively refine cluster assignments
      • Clustering with mixture of Gaussians
        • Expectation-maximization (EM) algorithm to maximize the log-likelihood
      • What if we have a batch of datasets to cluster?
   2. Clustering as a set-input problem
      • Input : X = \{ x_1, ..., x_n \}
      • Output : f(X) = (\pi, \mu, \sigma )
   3. Amortized inference in deep learning context
      • Express some non-trivial inference procedures as neural network evaluations. Knowledge from previous inferences are distilled in parameters of the neural networks
      • Old-school variational inference
        • q(z|x) are optimized for each x_i
          \prod^n_{i=1} q(z_i | x_i; \phi) = \prod^n_{i=1} N(x_i;\mu_i, \sigma^2_i)
      • Amortized variational inference
        • q(z_i | x_i ; \phi) = N(z_i; \mu_{\phi}(x_i), \sigma^2_{\phi}(x_i))
        • the inference procedure (approximating p(z_i | x_i;\theta) with q(z_i ; x_i;\phi) ) is expressed with the neural network evaluations ( \mu_{\phi}(\cdot), \sigma_{\phi}(\cdot))
   4. Amortized clustering
      • Reuse the previous inference (clustering) results to accelerate the inference (clustering) of new dataset.
   5. Solving amortized clustering for mixture of Gaussians
      • Build a permutation invariant f(\cdot;\phi) such as DeepSet architecture
      • DeepSets does not work well
        • Interaction between elements is crucial for clustering
4. Set Transformer
   1. Attention mechanism
      • Vaswani et al, Attention Is All You Need, NIPS 2017
      • Dot-product attention mechanism
        • Easy and efficient way to compute interactions between sets
          O = Att(X,Y) = softmax(\dfrac{QK^T}{\sqrt{d}})V 
      • Multihead QKV attention
        • Concatenate multiple attention with different weights to get more robust results
      • Self-attention
        • Attending to itself
        • efficiently encode pairwise interactions between elements in a set
        • self-attention is permutation equivariant
   2. Set Transformer
      • Lee et al, Set Transformer: A Framework for Attention-based Permutation-Invariant Neural Networks, ICML 2019
      • Permutation invariant neural network based on self-attention
      • Composed of a variant of transformer layer [Vaswani et al., 2017 ] that performs a permutation equivariant operation on sets
      • Building blocks
        • Multihead attention block (MAB)
        • Self-attention block (SAB)
        • Induced self-attention block (ISAB) : reduces time complexity to O(nm)
        • Encoder
          1. roughly matches to \phi(x) in DeepSets, transforms elements in a set into features in a latent space
          2. Composed of a stack of ISABs
          3. Efficient computation due to inducing points
        • Decoder
          1. Pooling by multihead attention (PMA) : instead of a simple sum/max/min aggregation, use multihead attention to aggregate features into a single vector
          2. Set input problems often require to produce multiple dependent outputs. (e.g. amortized clustering) In such case we utilize the self-attention mechanism in aggregation process
      • Properties
        • A Set transformer is at least as expressive as DeepSets, since it includes DeepSets as its special cases.
          
        • Nothing known about universality (but can represent any set input functions that a DeepSet can represent )
   3. Amortized clustering revisited
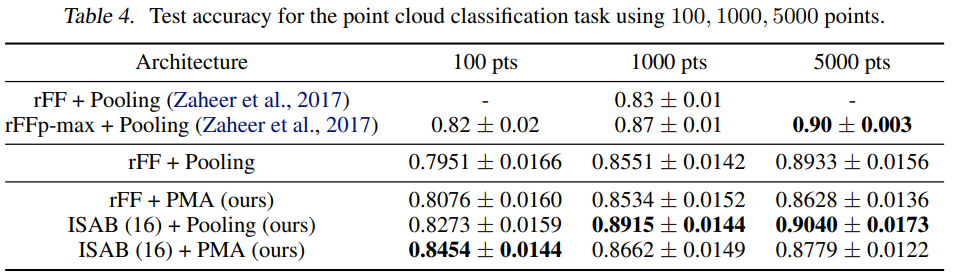
      • Set transformer solves amortized clustering accurately
        
   4.  Applications
      • Unique character counting
      • Anomaly Detection
   5. More complex clustering problems
      • Lee et al, Deep Amortized Clustering, arXiv 2019
        • Handling variable number of clusters
        • Handling non-trivial cluster shapes